|
mira digital 3


|
 Variables eclipsantes y cefeidas de corto período (2ª parte) Variables eclipsantes y cefeidas de corto período (2ª parte)
1ª parte de este artículo
Continuando un trabajo iniciado hace dos números, el autor expone las razones, técnicas y métodos para realizar un seguimiento pormenorizado de las variables eclipsantes y cefeidas de corto período.
Introducción:
Continuando con el artículo sobre las variables de tipo eclipsante y ceféidas de corto periodo, hemos dejado esta segunda parte para hablar más detalladamente sobre las razones que hacen de su observación una parte muy importante de la astronomía amateur y profesional. Hablaremos de otros tipos de curvas que nos ayudan a entender su comportamiento, para estas curvas hay todo un razonamiento matemático y estadístico que por desgracia me es desconocido y desconozco también las referencias para encontrarlo, así que he intentado explicarlo con más palabras y menos fórmulas, muy probablemente me equivoque en algunos razonamientos pero no creo estar muy lejos de la realidad. Invito a cualquiera que conozca esta base estadística y matemática a compartirla con nosotros.
Curvas en fase:
Comenzaremos hablando de un tipo de curva de luz un tanto diferente a la que normalmente se utiliza para el resto de las estrellas variables. Este tipo de curva de luz se llama curva en fase y se basa en la principal característica de las eclipsantes y ceféidas, “su periodicidad en un principio bien definida”. Es una curva que sigue representando en sus ejes de ordenadas y abcisas, magnitudes (visuales, fotométricas u otro tipo) y tiempo respectivamente.
Supongamos una variable cualquiera que presenta una curva de luz totalmente periódica sin ningún tipo de desfase, es decir, que cumple las efemérides al segundo. Utilizaremos como ejemplo la estrella binaria eclipsante Algólida prototipo (Beta Perseo, Algol). Para esta estrella y las de su tipo podemos obtener la curva de luz, sin observar necesariamente de forma continuada toda su variación, bastaría con transformar los puntos de las curvas de luz en distintos ciclos a un único ciclo.
Sirva de ejemplo la siguiente observación de esta estrella. Se han obtenido dos mínimos incompletos de Algol que representan dos ciclos separados de la estrella (ver la figura 1). Sin embargo, como muestra la figura 1 no tenemos el mínimo completo de la estrella, la curva en fase lo que hará será “unir” los puntos de las dos noches de observación en una única curva más completa y porque no decirlo, más bonita también. Para ello se tratan las fechas y horas de cada observación, más concretamente el día juliano, como un porcentaje del total del periodo de la estrella a representar, tomando como base o “cero” de la curva en fase cualquiera de los puntos de las curvas incompletas obtenidas, pero para mayor facilidad en este caso, tomaremos como punto cero la primera observación obtenida.
 Figura 1 Figura 1
Si tomamos este punto “cero” para empezar a representar la curva, los puntos que estén después de él irían aumentando el porcentaje total representado en la curva hasta llegar al 100% del periodo correspondiente de la estrella. Llegados al 100% del periodo en el eje x, los puntos de la curva que vamos a unir a esta primera parte y que pertenecen a otros ciclos, ya sean anteriores o posteriores, deben ser corregidos sumando o restando respectivamente el número de ciclos que han sucedido hasta el momento del punto cero elegido. En nuestro caso y de la forma que hemos tomado el punto “cero” tendremos que restar 2 ciclos a las observaciones de la segunda parte de la curva de luz para unirlas al resto de la curva en fase, puesto que por medio hay otro mínimo que no se observó. En definitiva, se trata de convertir el día juliano de las observaciones a un porcentaje de la curva de luz. Por ello, lo más importante y para obtener la curva lo más exactamente posible, debemos disponer del dato del periodo de la estrella con cuantos más decimales de exactitud mejor, así como las fechas julianas con el mismo número de decimales que el periodo, este número de decimales será también el margen de errorobtenido en la representación de la curva, sin tener en cuenta claro, los errores inherentes a la observación en sí.
Mostramos a continuación las fórmulas adecuadas para esta transformación, para los dos casos en que las observaciones estén realizadas antes del “cero” de referencia o posteriores:
Para observaciones posteriores al cero de referencia:
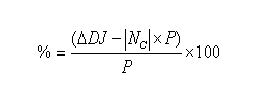
Para observaciones anteriores al cero de referencia:
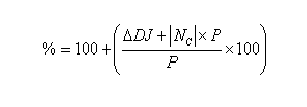
NC= Número de ciclos transcurridos entre los dos mínimos observados, en valor absoluto.
P= Período de la estrella.
DDJ= Incremento de día Juliano.
Así facilitamos la obtención de curvas de variables con periodos de muchas horas. Pero además de esta ventaja, la curva en fase supone una curva de luz mucho más poblada de puntos y por tanto, mayor exactitud para determinar la amplitud media de la estrella, durante los ciclos representados en ella. Sin embargo, la curva en fase no nos ayuda mucho para determinar si la estrella está cumpliendo perfectamente las efemérides, o lo que es lo mismo, saber si su periodo está teniendo un valor fijo o por el contrario está cambiando. Este es el cometido de otro tipo de curva utilizada en estas variables, la curva O-C (Observada-Computerizada). Bien es cierto, que para una estrella de la que conocemos su periodo por catálogos, una curva en fase basada en ese periodo si no muestra la curva perfectamente es indicativo de que el periodo ha variado y por tanto la curva en fase también nos puede servir como un primer acercamiento al valor de la variación del periodo. La figura 2 muestra el resultado de la curva en fase tomando como base el periodo dado en el GCVS.
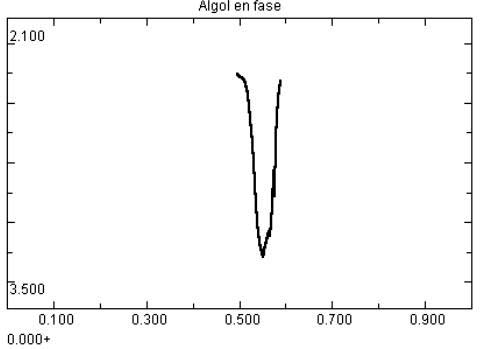
Figura 2
Curva O-C:
La curva O-C se basa en la hipótesis de que el periodo de la estrella es realmente constante y pondrá de manifiesto si ésta hipótesis es cierta realmente para cada estrella.
Al igual que en la curva en fase se toma un punto inicial de referencia, en este caso no es un punto de la curva de luz sino una época de mínimo o máximo, es decir una fecha en la que ha ocurrido un mínimo o un máximo de la estrella. Esta fecha representa el cero en el eje de ordenadas (y) que representará días o más bien, pequeñas fracciones de día y también es el cero para el eje de absisas (x), el cual muestra los ciclos de la estrella. La fecha que se suele tomar es la dada por el Catálogo General de Estrellas Variables (GCVS). En esta curva, una estrella observada en muchos mínimos posteriores a la época del GCVS, cuyo periodo no tenga variaciones dibujará exactamente una línea recta. Una estrella cuyo periodo varíe puede dibujar distintos tipos de curvas según sea esa variación, puede ser lineal ascendente, descendente, parabólica, etc, de esta manera adaptando una función lo más acertada posible a la curva, podremos obtener una forma para calcular las nuevas efemérides de la estrella, aun cuando el periodo sea variable. El eje x es inmediato solo es necesario saber el periodo de la estrella, es el eje y el que realmente “dibuja la curva”.
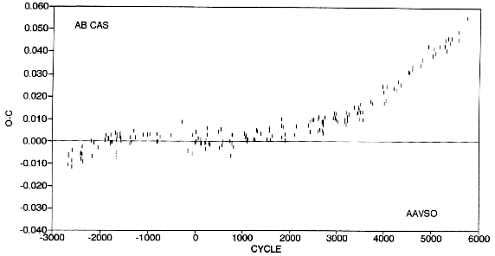
Figura 3
El eje y es realmente el incremento o decremento que ha tenido lugar en el periodo de la estrella desde la época de referencia, hasta los distintos ciclos observados. Cuantos más ciclos observemos más puntos tendremos en la curva O-C y mejor será la línea o curva que se adaptará y así, más exactas serán las nuevas efemérides. Para obtener el incremento del periodo aplicaremos la siguiente fórmula:
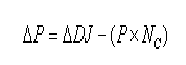
La curva O-C es una herramienta muy buena para todo variabilista, que busca algo más que obtener una curva de luz bonita de una variable, pues nos permite con solo nuestras propias observaciones, que determinemos si una variable está cambiando su periodo. Para obtener la función adecuada a la nube de puntos de la curva O-C, se adaptan generalmente ecuaciones de primer y segundo orden, que lógicamente calculara un programa de ordenador.
Otro tema ahora, es explicar el porqué de estas variaciones y porqué se adaptan precisamente a esas curvas. Una función lineal ascendente o descendente, significa que el periodo está aumentando o disminuyendo respectivamente, lo que podría ser provocado porque las dos estrellas (en el caso de una eclipsante) se están separando o acercando la una de la otra a una velocidad constante, respectivamente. Una función parabólica implica un cambio no lineal en el periodo, así que la velocidad no será constante. Pueden existir muchas explicaciones físicas, que el ángulo de visión de la eclipsante esté oscilando, la forma de las estrellas cambie por ejemplo, de circular a elíptica y muchas otras. En el caso de una ceféida el proceso no es externo a la propia estrella sino interno, la variación del periodo estará relacionado con la evolución de la estrella, y su estudio mejora la teoría sobre la evolución estelar. En fin, esto es ya materia de los teóricos, entre los cuales no me encuentro, por lo menos no de momento.
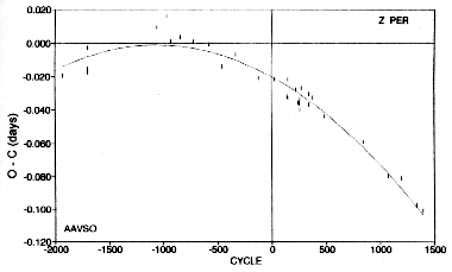
Figura 4
Aunque la curva O-C es muy utilizada para variables eclipsantes y ceféidas, es también muy útil para encontrar periodos de variación o modelos de variación en otras variables, como Novas, Supernovas, Miras, variables Cataclísmicas y cualquiera que pueda mostrar un fenómeno periódico. La curva O-C es aplicable realmente a cualquier fenómeno que sea periódico, incluso a la hora de llegada del autobús a vuestra parada.
Bibliografía:
- Journal AAVSO Vol 26, nº1 1997.
- Observed Minima Timings of Eclipsing Binaries, nº 4 . AAVSO.
Máximo Suárez Tejera
|

