A Model of Sustainable Development opposite to the Ecological Hecatomb.
Vicent
Castellar-Busó i Rafael Pla-López
Departament de Matemŕtica Aplicada
Universitat de Valčncia
Introduction: the model.
We work with an Adaptive, Historical, Geographical and Multidimensional Model with Resignation built from a General Learning Theory which is formulated in terms of General Systems Theory. By means of this Mathematical Model, we have studied the possible paths of evolution from a Full Repressive Society to a Free Scientific Society with a multidimensional state-variable which values characterise social behaviours.
The Model is composed by means of the interaction of several mathematical Systems, which express the relations between the variables involved:
The core of the Model is the Learning System, through positive and negative reinforcement: the probability (P) of each social behaviour (U), in each individual subsystem (N) of a social population, increases when his goal is fulfilled and decreases when it is not fulfilled from this social behaviour. If no social behaviour available to an individual subsystem produces goal fulfilment, then this subsystem can be destroyed. The fulfilment probability (PG) depends on its technical possibility (p), which is weighted by a factor determined by the social organisation (1 – s).
This factor is generated by a Repression System: each social behaviour, according to its scope (F) in each individual subsystem, the impact (I) of this on different individual subsystems, and its repressive capacity (k), produces a decrease of this factor for the different social behaviours. Thus, each social behaviour represses the other social behaviours, by decreasing its goal fulfilment.
A Relay System produces a random (a) substitution (g) of an individual subsystem for a "child subsystem" with initial equiprobability (natalis) of every available social behaviour. A "child subsystem" can also occupy (A) the niche of a destroyed subsystem. Thus, relay causes the loss of the information accumulated in the substituted individual subsystem.
Also, a Science System determines the probability of learning (PL) for each social behaviour in each subsystem: the probability of the experience of other subsystems, which is weighted by factors of emission, reception and impact, is added to its own experience. This System expresses the relations of intellectual communication between different individual subsystems.
A Historic System simulates historical evolution through the random (b) increase (d) of the dimension (m) of the state-variable in each subsystem, and therefore of the number of its available social behaviours. The probability of evolution is increased (b) by the existence of social behaviours, which were theoretically not available but are forced by the Science System from the experience of other subsystems. This System expresses technological progress and technological diffusion (we characterise a technologically higher society by a greater capacity of choice between different social behaviours).
An Adaptive System determines the dynamic evolution (Ta) of the repressive capacity in a subsystem, from an initial value (k) -when it is a "child subsystem"- which depends on the might (m), associated to the technological level, and ferocity (g) of the social behaviour-, toward its suffered repression (s). The Adaptation Time Ta expresses the delay in the adaptation of produced repression (s) to suffered repression (s). Thus, with a low delay Ta, the produced repression equals quickly the suffered repression. On the contrary, with a high delay Ta, produced repression remains approximately constant.
A Resignation System expresses the influence of subjective factors through a tendency to a statistical normalisation of the reinforcement from satisfaction and dissatisfaction. We name this tendency "resignation", and express it by a time of delay (Tr) according to a model of Systems Dynamics.
Moreover, a Delay System expresses the decrease of Adaptation Time Ta with might µ, the increase of Resignation Time Tr with ferocity n, by means of the parameters Ka and Kr respectively. Moreover, time Te increases with ferocity and decrease with might by means of a parameter Ke. An Impact System expresses how the impact I on repression and intellectual communication depend on might m and distance (d) between subsystems.
A Natural System expresses a diversity of initial condition natalis of the individual subsystems. In its first version, this System is a rigid System, without neither feedback nor evolution.
The Second Principle of Thermodynamic.
In previous projects the corresponding satisfaction to each social behaviour was depending on a function of the different social behaviours that were designated technical possibility of satisfaction and on a factor to reduce the satisfaction when the suffered repression increased.
In this work, we take that function as a technical possibility of initial satisfaction, which we represent by p0(U), and we add a new factor to obtain the current technical possibility of satisfaction. With this new factor we wish to introduce the increase in entropy that is produced through the manipulation of energy and information. Thus, we introduce the cost that corresponds to a fraction of the energy that is dissipated and to a portion of the information that is lost.
The most developed behaviours are characterised by an upper quantity of transformations of resources in which the energy is dissipated, and by an upper transmission of information, and, therefore, by an upper increase of the entropy.
On the other hand, the entropy
reduces with the concentration of the behaviours, that is to say,
the entropy reduces with the repression. Thus, the technical
possibility of satisfaction remains
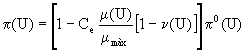
Ecology and recycling.
With the ecology, we wish to represent the degradation of the environment as a consequence of the consumption in satisfaction and repression. Also, it is associated to a decrease in the possibility of consumption, in satisfaction as well as in repression, in order to recover the environment through the recycling.
We will represent the ecology through a global not negative variable E. It starts from an initial value E0 sufficiently great to maintain, during the whole evolution, so much consumption in satisfaction or in repression as the whole of the active subsystems could do. Even, the sum of these consumptions can arrive at its maximum level simultaneously, but it will not be able to stay there by the degradation that the environment would suffer. This variable can arrive to the value zero, situation that we will designate as ecological hecatomb. A value that permits this situation is E0 = 2NP.
The consumption in satisfaction and repression contributes to the decrease of the resources, that is to say, of the ecology. It is necessary to define and to characterise the processes which would also permit the increase of this variable, always between their extremes. These processes will be the reutilization and the recycling.
According to our model, the reutilization does not imply any cost at all. Otherwise, the recycling is characterised by a cost that causes a decrease in the consumption in satisfaction, in repression or in both. Actually, we can assimilate the real cost of the reutilization to the recycling and associate the reutilization to the natural cycles and to the crops. We will represent the reutilization and the recycling by r and r respectively.
The expressions of the
consumption in satisfaction and in repression, and the cost of
the recycling are
K2 = SN,U s(U,N)P(U,N) and
K3 = SN,U r(U,N)P(U,N) respectively.
Moreover, the effects of the consumption on the ecology are global; thus we will consider that its influence on the environment is equally expressed for any social behaviour in each subsystem.
As the reutilization is associated with the natural cycles, it is bounded by a fraction of the available resources according to a factor Cl. The variation of this factor will be object of study in this work. Also, we consider that it is bounded by the consumption in satisfaction and in repression and it cannot be negative. The expression r = max[0, min[Cl·E, E0 – E + K1 + K2]] gives us the value of the reutilization.
The recycling is formulated according to an ideal value which corresponds to the consumed and not reutilized resources and it cannot be negative. Thus, we express the ideal recycling by rI = max[0, min[E0 – E – r +K1 +K2, E0].
We will apply a delay ![]() where Ke is an
ecological parameter.
where Ke is an
ecological parameter.
Finally, we consider that the maximum possible cost in recycling corresponding to each social component is bounded by its possibilities of consumption.
Thus,
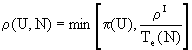 and
and
Furthermore, the interaction
with the environment modifies the satisfaction, represented as PG(U;N),
for each social behaviour in each subsystem, increasing with the
recovery of the environment but decreasing with the cost of the
produced recycling, according to ![]() .
.
Specification of the Model.
We work with NP = 40 individual subsystems, a maximum dimension mmax = 4 and binary components Ui Î {0,1} of the social behaviour U.
With this specification, U = (0000) would correspond to a Primitive Society with a technical possibility of satisfaction equal to 0, without scientific communication, and which has ferocity but not might, and therefore has no repressive capacity.
In the same way, U = (0111) = 7 corresponds to a Full Repressive Society with technical possibility of satisfaction p = ľ, some scientific communication and full repressive capacity k = 1.
Finally, U = (1111) = 15 = F corresponds to a Free Scientific Society with full technical possibility of satisfaction p = 1, full scientific communication and null repressive capacity k = 0.
We speak about predominance of a state U0 if its probability is the majority [P(U0) > ˝] in a relative majority of subsystems. In add, we speak about strong predominance if moreover its probability of satisfaction (PG) is the maximum.
We are especially interested in processes of evolution with strong predominance of a Full Repressive Society [U = (0111)], by considering that only such processes can simulate the real social evolution on the Earth planet, from current New International Order supported in last chance on nuclear armament. And we wish to find the conditions that facilitate the overcome of this situation.
Also, we wish to study the recovery of the environment after the deterioration associated with the repressive societies.
In the present work we will study how these situations are distributed according to the values that the parameters Cl and Ce take.
We have implemented our model in language C and we have executed it 4.320 times with different initial conditions.
Results.
We summarise the results in the table
|
The Full Repressive System doesn’t reach the Strong Predominance |
The Full Repressive System reaches and maintains the Strong Predominance |
The Full Repressive System reaches the Strong Predominance but it doesn’t maintain it |
Ecological Hecatomb |
0% |
36’12% |
6’15% |
Sustainable Development |
24’58% |
23’84% |
9’31% |
pstrong = 0’5360·ln(Ce) – 0’1411·ln(0,1·Cl + 0’1979 for R = 0’9521 as better fitting.
The 15’46% of the evolutions
go through the strong predominance phases and surpasse it. The
distribution of these evolutions relative to the parameters Ce
and Cl it is the normal function
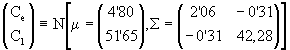 .
.Also, we have studied the proportions in which the ecological hecatomb is produced and the proportions in which the ecological recovery is completed. In this case we have obtained respectively the fittings
p0 = 0’3260·ln(Ce) – 1’0092·ln(0,1·Cl)+ 1’5981 for R = 0’9394 and
p1 = –0’1563·ln(Ce) + 1’6041·ln(0,1·Cl)– 2’0983 for R = 0’8131.
The proportion of evolutions that ends with a partial recovery of the ecology has not admitted any satisfactory fitting, but it is expressed by q = 1 – p0 – p1.
Sustainable development and consumption.
We show the trajectory of the consumption in satisfaction, repression and recycling of an evolution that ends in Ecological Hecatomb (Figure 1) and of other evolution that gets be maintained within Sustainable Development (Figure 2).
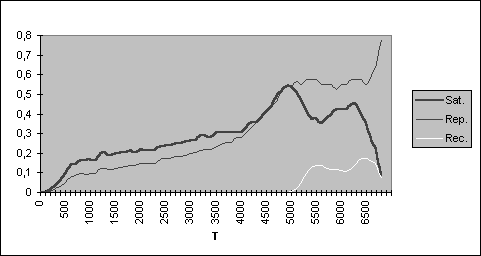
Figure 1
Evolution of the consumption in presence of the Ecological Hecatomb
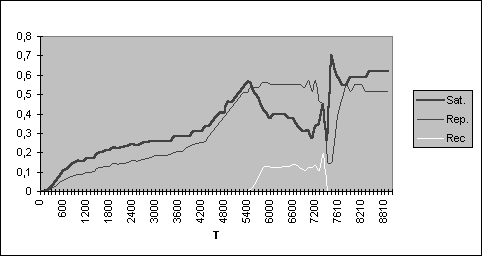
Figure 2
Evolution of the consumption in absence of the Ecological Hecatomb
Ecology and "revolt"effects.
In previous projects, we were
studying the appearance of improbable behaviours
associated with evolutions in those the strong dominance was
appearing and with low values of PG. We recall that
now 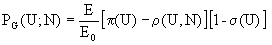 . Thus, the
reduction of the resources and the cost of the recycling make
more probable the appearance of these effects. However, with the
modifications of the introduced model, we have only obtained
quantitative changes in the appearance frequency, but not
qualitative changes in its causes or consequences.
. Thus, the
reduction of the resources and the cost of the recycling make
more probable the appearance of these effects. However, with the
modifications of the introduced model, we have only obtained
quantitative changes in the appearance frequency, but not
qualitative changes in its causes or consequences.
Interpretation and conclusions.
We have included in our model the parameter Ce to represent the cost of the dissipation of an fraction of the energy according to the Second Principle of the Thermodynamic and the parameter Cl to represent the efficiency in the reutilization of resources associated with the natural cycles.
The variation of the parameters Ce and Cl provides a monotonous variation of the ecological recovery, from the Ecological Hecatomb (when these parameters are very adverse) until the automatic recovery (when they are very good). In the intermediate zone prevails the partial recovery of the resources.
Also, we observe that the consolidation of restrictive social behaviours increases with the adversity of the parameters. However, the possibility of surpassing this restrictive phase does not present monotony with the parameters Ce and Cl: it is accumulated about the point (Ce, Cl) = (4’80, 51’65).
The modification of the model only provides a quantitative change on the appearance of improbable behaviours (revolt effect). Now, its cause –the decreasing of the resources when the parameters are adverse– is more frequent but we do observe neither new causes nor new effects.
Upon comparing the Figures 1 and 2 we observe, in the Sustainable Development, consumption constant in which the satisfaction increases when the repression decreases. Other ways conclude in the Ecological Hecatomb.
References.
1. Atkins P. W. (1986): "The Second Law", Freeman, New York y Londres.
2. Campbell, B. (1994) "Human Ecology", Hinemann Educational Books Ltd., Londres.
3. Klir, G. J. (1969) "An Approacho to General System Theory", D. Van Nostrand Co., Londres.
4. Margalef, R. (1981) "Ecología", Ed. Planeta, Barcelona.
5. Tamames, R. (1995): "Ecología y Desarrollo Sostenible: La Polémica Sobre los Límites del Crecimiento. (6Ş edición revisada y ampliada) Alianza Editorial, Madrid.
6. Pla-López, R. (1988): "Introduction to a Learning General Theory", Cybernetics and Systems: An International Journal 19, 411-429.
7. Pla-López, R & Castellar-Busó V. (1994) "Model of Historical-Geographical Evolution", in R. Trappl ed., Cybernetics and Systems’94, I, World Scientific, Singapore, 1049-1056.
8. Pla-López, R (1996): "Cuánto Puede Perdurar una Revuelta", I Reunión Espańola de Ciencias de Sistemas, Valčncia, Ab. 17-19
9. Pla-López, R. (1996): "Social and Ecological Consequences of Adaptive Pacifism and Unsubmission", 3e Congrčs Europeén de Systémique, Roma, Oc. 1-4.