Un modelo de desarrollo sostenible opuesto a la hecatombe ecológica.
Vicent
Castellar-Busó & Rafael Pla-López
Departament de Matemàtica Aplicada
Universitat de València
Introducción: El modelo.
Trabajamos con un modelo matemático adaptativo, histórico, geográfico y multidimensional construido a partir de una Teoría General del Aprendizaje formulada en términos de Teoría General de Sistemas. Mediante dicho modelo matemático hemos estudiado las posibles vías de evolución de una sociedad plenamente represiva a una sociedad científica libre con una variable de estado multidimensional cuyos valores caracterizan los comportamientos sociales.
El modelo se compone de la interacción de varios sistemas matemáticos que expresan las relaciones entre las variables involucradas:
El núcleo del modelo es el sistema de aprendizaje probabilístico mediante refuerzo positivo y negativo: la probabilidad (P) de cada comportamiento social (U) en cada subsistema individual (N) de una población social aumenta cuando sus objetivos se cumplen y disminuye cuando no se cumplen desde dicho comportamiento social. Si ningún comportamiento social disponible para un subsistema individual lleva al cumplimiento de los objetivos, entonces dicho subsistema puede destruirse. La probabilidad de cumplimiento de los objetivos (PG) depende de su posibilidad técnica (p) y de un factor determinado por la organización social (1-s).
Este factor se genera por un sistema de represión: cada comportamiento social, de acuerdo con su alcance (F) en cada subsistema individual, produce una disminución de dicho factor para los comportamientos sociales diferentes. Así, cada comportamiento social reprime los otros comportamientos sociales, disminuyendo su cumplimiento de objetivos.
Un sistema de relevo produce una sustitución (g) aleatoria (a) de un subsistema individual por un subsistema neófito con equiprobabilidad inicial (kntl) de todos los comportamientos sociales disponibles. Un subsistema neófito puede también ocupar (A) el nicho de un subsistema destruido. Así, el relevo causa la pérdida de la información acumulada en los subsistemas individuales sustituidos.
También, un sistema de ciencia determina la probabilidad de aprendizaje (PL) para cada comportamiento social en cada subsistema: la probabilidad derivada de la experiencia de los otros, ponderada por factores de emisión, recepción e impacto (I), es añadida a su propia experiencia. Este Sistema expresa las relaciones de comunicación intelectual entre diferentes subsistemas individuales.
Un sistema histórico simula una evolución histórica a través del aumento (d) aleatorio (b) de la dimensión (m) de la variable de estado, y por lo tanto del número de comportamientos sociales disponibles. La probabilidad de evolución de un subsistema se incrementa (b) por la existencia de comportamientos sociales que teóricamente no estarían disponibles para él pero que son forzados por el sistema de ciencia a partir de la experiencias de otros subsistemas. El sistema histórico expresa el progreso tecnológico, y también la difusión de tecnologías (caracterizamos una sociedad tecnológicamente avanzada por una mayor capacidad de elección entre distintos comportamientos sociales).
Un sistema de adaptación determina la evolución dinámica (Ta) de la capacidad represiva en un subsistema, a partir de un valor inicial (k) cuando es un subsistema neófito -el cuál depende de la fuerza (µ) y la ferocidad (n) del comportamiento social-, hacia la represión sufrida por el mismo (s). El tiempo de adaptación Ta expresa el retraso en la adaptación de la represión producida (s) a la represión sufrida (s): así, con un retardo Ta bajo, la represión producida tiende rápidamente a igualar la represión sufrida; por el contrario, con un gran retardo Ta, la represión producida varía lentamente.
Un sistema de resignación expresa la influencia del factor subjetivo a través de la tendencia a una normalización estadística del refuerzo a partir de la satisfacción e insatisfacción; llamamos a dicha tendencia resignación, y la expresamos por un tiempo de retardo (Tr) de acuerdo con un modelo de dinámica de sistemas.
Un sistema de impacto expresa cómo el impacto I sobre la represión y la comunicación intelectual depende de la fuerza (µ) y de la distancia (d) entre subsistemas.
Un sistema natural expresa una diversidad de condiciones iniciales kntl de los subsistemas individuales. En su primera versión, dicho sistema es rígido, sin retroalimentación ni evolución.
Finalmente, hemos reformulado el sistema ecológico. Expresa una destrucción ecológica (E<E0) a través de la disminución de las posibilidades técnicas de satisfacción p cuando la suma de las capacidades represivas s y de las posibilidades técnicas de satisfacción p sobrepasa a la suma de reutilización. La destrucción ecológica puede ser revertida con un retraso Te mediante un coste en reciclaje.
El Segundo Principio de la Termodinámica.
En trabajos anteriores la satisfacción correspondiente a cada comportamiento social dependía de una función de los diferentes comportamientos sociales que denominábamos posibilidad técnica de satisfacción y de un factor con el que se reducía la satisfacción cuando aumentaba la represión sufrida.
En este trabajo, tomamos aquella función como posibilidad técnica de satisfacción inicial, la cual representamos p0(U), y añadimos un nuevo factor para obtener la actual posibilidad técnica de satisfacción. Con este factor deseamos introducir el aumento de entropía que se produce en la manipulación de energía y de información. Así, introducimos el coste que corresponde a una fracción de la energía que se disipa y a una parte de la información que se pierde.
Como los comportamientos más desarrollados se caracterizan por una cantidad mayor de transformaciones de los recursos, transformaciones en las que se disipa la energía, y por una mayor transmisión de la información, les corresponde un aumento mayor en la entropía.
En cambio, la entropía disminuye con la reducción de comportamientos diferentes, es decir, la entropía disminuye con la represión. Así, la posibilidad técnica de satisfacción queda
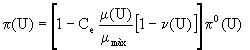
donde Ce es un parámetro entrópico que toma valores en un conjunto de condiciones iniciales y cuya variación estudiaremos en este trabajo
Ecología y reciclaje.
Con la ecología deseamos representar la degradación del entorno como consecuencia del consumo en satisfacción y como consecuencia de la represión. También tiene asociada una disminución en la posibilidad de consumo, tanto en satisfacción como en represión, para poder recuperar el entorno mediante el reciclaje.
Representaremos la ecología mediante una variable global E no negativa, la cual partirá de una valor inicial E0 suficientemente elevado como para que sea posible mantener durante toda la evolución un consumo en satisfacción o un consumo en represión tan alto como sean capaces la totalidad de los sistemas activos. Incluso la suma de estos consumos pueden llegar al nivel máximo simultáneamente, pero no podrán permanecer así por la degradación que sufriría el entorno. Esta variable puede llegar al valor cero, situación que denominaremos hecatombe ecológica. Un valor que permite esta situación corresponde a E0 = 2·NP.
Como el consumo en satisfacción y el consumo en represión contribuyen a la disminución de los recursos, es decir de la ecología, es necesario definir y caracterizar los procesos mediante los cuales sea posible también el aumento de esta variable, siempre entre sus extremos. Estos procesos son la reutilización y el reciclaje.
Diferenciamos la reutilización del reciclaje en que la primera no conlleva un coste que sí caracteriza al segundo. Este coste ocasiona una disminución en el consumo en satisfacción, en represión o en ambos. Realmente, podemos asimilar el coste de la reutilización al reciclaje y asociar la reutilización a los ciclos naturales y a las cosechas. Representaremos a la reutilización y al reciclaje r y r respectivamente.
Las expresiones de los consumos en satisfacción y en represión y del coste del reciclaje son respectivamente
K1 = SN,U p(U)P(U,N),
K2 = SN,U s(U,N)P(U,N) y
K3 = SN,U r(U,N)P(U,N).
Además, como los efectos del consumo sobre la ecología son globales consideraremos que la influencia sobre el entorno se expresa de la misma forma para cualquier comportamiento social y en cualquier sistema.
Como la reutilización está asociada a los ciclos naturales, en este sentido está acotada por una fracción de los recursos disponibles según un factor Cl. La variación de este factor será objeto de estudio en este trabajo. También consideramos que está acotada por los consumos en satisfacción y en represión y no puede ser negativa. La expresión r = máx[0, mín[Cl·E, E0 – E + K1 + K2]] nos da el valor de la reutilización.
El reciclaje se formula respecto a un valor ideal, el cual corresponde a los recursos consumidos y no reutilizados y tampoco puede ser negativo. Así, expresamos el reciclaje ideal mediante rI = máx[0, mín[E0 –E – r +K1 +K2, E0].
Aplicaremos un retardo
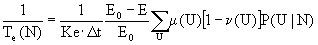
donde Ke es un parámetro que puede variar en un conjunto de condiciones iniciales.
Finalmente, también consideramos que el máximo coste posible en reciclaje correspondiente a cada componente social está acotado por sus posibilidades de consumo.
Así,
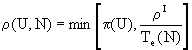
y
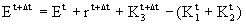
Además, las relaciones con el entorno hacen variar la satisfacción, representada como PG(U;N), para cada comportamiento social en cada sistema, aumentando con la recuperación del entorno pero disminuyendo con el coste del reciclaje producido, según
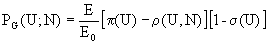
Especificación del Modelo.
Trabajamos con NP = 40 subsistemas individuales, una dimensión máxima mmax = 4 y componentes binarios UiÎ{0,1} del comportamiento social U.
Con dicha especificación, U = (0000) puede corresponder a una sociedad primitiva con posibilidad técnica de satisfacción nula, sin comunicación científica, la cual tiene ferocidad pero no fuerza, y por lo tanto no tiene capacidad represiva.
Así mismo, U = (0111) puede corresponder a una sociedad plenamente represiva con alguna posibilidad técnica de satisfacción inicial p0 = ¾, alguna comunicación científica y plena capacidad represiva k = 1.
Finalmente, U = (1111) corresponde a una Sociedad Científica Libre con plena posibilidad técnica de satisfacción inicial p0 = 1, plena comunicación científica (factores de emisión y recepción máximos) y nula capacidad represiva inicial k = 0.
Hablamos de predominio de un estado U0 si su probabilidad es mayoritaria [P(U0) > ½] en una mayoría relativa de subsistemas. Y hablamos de predominio fuerte si además su probabilidad de satisfacción es la máxima [PG(U0) = máxU PG(U)].
Estamos especialmente interesados en procesos de evolución con predominio fuerte de una Sociedad Plenamente Represiva [U = (0111)], por considerar que sólo tales procesos pueden simular la evolución social real sobre el planeta Tierra, a partir del actual Nuevo Orden Internacional apoyado en última instancia en armamento nuclear. Y deseamos encontrar las condiciones que faciliten la superación de esta situación.
También deseamos estudiar la recuperación del entorno después del deterioro asociado a las sociedades represivas.
En el presente trabajo estudiaremos cómo se distribuyen estas situaciones según los valores que tomen los parámetros Cl y Ce.
Con este fin hemos implementado nuestro modelo en lenguaje C y lo hemos ejecutado 4.320 veces con distintas condiciones iniciales Cl y Ce.
Resultados.
Resumimos los resultados en la tabla
No se alcanza el dominio fuerte |
Se mantiene el dominio fuerte |
Se supera el dominio fuerte |
|
Hecatombe ecológica |
0% |
36’12% |
6’15% |
Desarrollo sostenible |
24’58% |
23’84% |
9’31% |
Representamos las proporciones en que se ha llegado al dominio fuerte y las proporciones en que después de llegar al dominio fuerte se ha superado en las figuras 1 y 2. En el primer caso, hemos ajustado mediante mínimos cuadrados la evolución de las proporciones y después de comparar una amplia familia de transformaciones –logarítmicas, exponenciales, cuadráticas, inversamente proporcionales, trigonométricas y ciclométricas– hemos obtenido como mejor ajuste
pfor = 0’5360·ln(Ce) – 0’1411·ln (0’1·Cl) + 0’1979 con R = 0’9521.
El 15’46% de las evoluciones pasaban por la fase de dominio fuerte y la superaban. La distribución de estas evoluciones respecto a los paràmetros Ce y Cl es
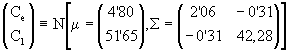
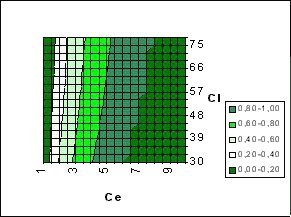
Figura 1
Proprción en que se alcanza el Dominio Fuerte
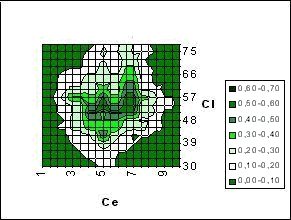
Figura 2
Proprción en que se supera el Dominio Fuerte
También hemos estudiado las proporciones en que se produce la hecatombe ecológica y las proporciones en que la recuperación ecológica es completa (Figs. 3 y 4). En este caso hemos obtenido respectivamente los ajustes
p0 = 0’3260·ln(Ce) – 1’0092·ln(0’1·Cl) + 1’5981 con R = 0’9394 y
p1 = –0’1563·ln(Ce) + 1’6041·ln(0’1·Cl) – 2’0983 con R = 0’8131.
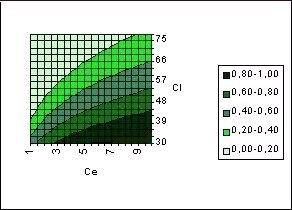
Figura 3
Proprción de presencia de Hecatombe Ecológica
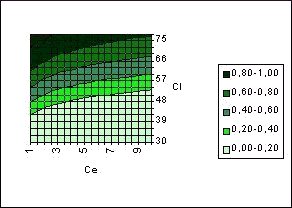
Figura 4
Proprción en que la recuperación ecológica es completa
La proporción de evoluciones que finalizan con una recuperación parcial de la ecología no ha admitido ningún ajuste satisfactorio, per queda bien definida como el resto (hasta la unidad) de las ya ajustadas, es decir, q = 1 – p0 – p1.
Desarrollo sostenible y consumo.
Una vez halladas las zonas de los parámetros que facilitan o dificultan la recuperación ecológica (o alternativamente la hecatombe ecológica), mostramos la trayectoria de los consumos per capita en satisfacción, represión y reciclaje de una evolución que finaliza en hecatombe ecológica (Fig. 5) y de otra que consigue mantenerse dentro del desarrollo sostenible (Fig. 6).
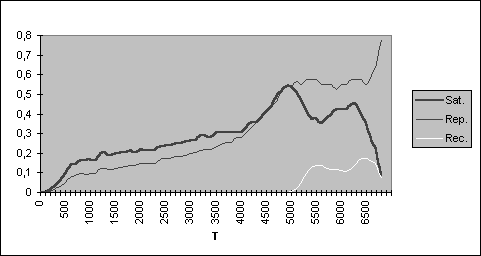
Figura 5
Evolución del consumo en presencia de la Hecatombe Ecológica
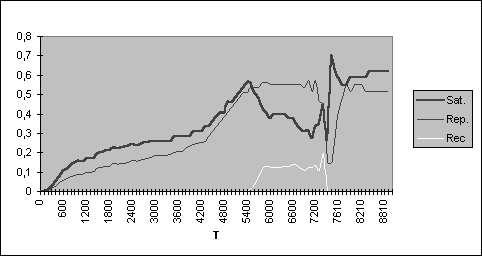
Figura 6
Evolución del consumo en ausencia de la Hecatombe Ecológica
Ecología y efectos "revuelta".
En trabajos anteriores estudiábamos la aparición de comportamientos poco probables asociados a evoluciones en las que aparecía el dominio fuerte y a valores bajos de PG . Recordemos que ahora
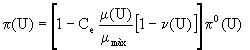 .
.
Así, tanto la reducción de los recursos como el coste del reciclaje hacen más probable la aparición de estos efectos. Sin embargo, con las modificaciones del modelo introducidas, sólo hemos obtenido cambios cuantitativos en la frecuencia de apariciones, pero no cambios cualitativos en sus causas o consecuencias
Interpretación y conclusiones.
Hemos incluido en nuestro modelo los parámetros Ce y Cl para representar respectivamente el coste de la disipación de una fracción de energía en virtud del Segundo Principio de la Termodinámica y la efectividad en la reutilización de recursos asociada a los ciclos naturales.
Al variar sus valores obtenemos también una variación monótona del grado de recuperación ecológica que va desde la hecatombe ecológica cuando estos parámetros son muy adversos hasta la recuperación automática cuando son muy favorables. En la zona intermedia predomina la probabilidad de recuperación parcial de los recursos.
También observamos que la consolidación de comportamientos sociales represivos aumenta con la adversidad de los parámetros. Sin embargo, la posibilidad de superar esta fase represiva no presenta monotonía con los parámetros Ce y Cl: Se acumula alrededor del punto (Ce,Cl) = (4’80, 51’65) (ver Figura 2).
Respecto a la aparición de comportamientos poco probables (efecto revuelta), la modificación del modelo sólo proporciona un cambio cuantitativo al hacer más frecuente el proceso que los origina –disminución de los recursos cuando los parámetros son adversos–, pero no observamos ni causas ni efectos nuevos.
Al comparar las Figuras 5 y 6 observamos en el desarrollo sostenible un consumo per capita constante en el cual aumenta la satisfacción al reducirse la represión. Otras tendencias concluyen en la hecatombe ecológica.
Bibliografía.
Atkins P. W. (1986): "The Second Law", Freeman, New York y Londres.
Campbell, B. (1994) "Human Ecology", Hinemann Educational Books Ltd., Londres.
Klir, G. J. (1969) "An Approacho to General System Theory", D. Van Nostrand Co., Londres.
Margalef, R. (1981) "Ecología", Ed. Planeta, Barcelona.
Tamames, R. (1995): "Ecología y Desarrollo Sostenible: La Polémica Sobre los Límites del Crecimiento. (6ª edición revisada y ampliada) Alianza Editorial, Madrid.
Pla-López, R. (1988): "Introduction to a Learning General Theory", Cybernetics and Systems: An International Journal 19, 411-429.
Pla-López, R & Castellar-Busó V. (1994) "Model of Historical-Geographical Evolution", in R. Trappl ed., Cybernetics and Systems’94, I, World Scientific, Singapore, 1049-1056.
Pla-López, R (1996): "Cuánto Puede Perdurar una Revuelta", I Reunión Española de Ciencias de Sistemas, València, Ab. 17-19.
Pla-López, R. (1996): "Social and Ecological Consequences of Adaptive Pacifism and Unsubmission", 3e Congrès Europeén de Systémique, Roma, Oc. 1-4.