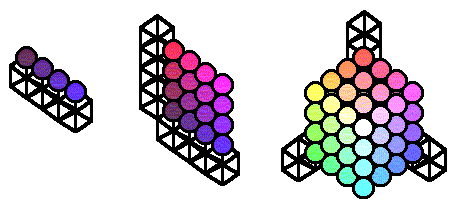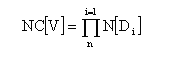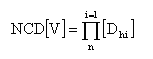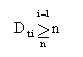|
Cómo diseñar grandes variables en bases de datos multidimensionales
Manuel de la Herrán Gascón Vicent
Castellar
IntroducciónEl uso de dimensiones es una forma de mostrar (y a veces almacenar) datos muy útil en sistemas con grandes cantidades de información. Las dimensiones son ejes de análisis o criterios de clasificación de la información que ofrecen un índice a los datos mediante una lista de valores. Por ejemplo son dimensiones <Tiempo>, <Geografía> y <Producto>. Se llama DataWarehouse al almacén de datos que reúne la información histórica generada por todos los distintos departamentos de una organización, orientada a consultas complejas y de alto rendimiento. Un DataWarehouse pretende conseguir que cualquier departamento pueda acceder a la información de cualquiera de los otros mediante un único medio, así como obligar a que los mismos términos tengan el mismo significado para todos. Un Datamart es un almacén de datos históricos relativos a un departamento de una organización, así que puede ser simplemente una copia de parte de un DataWarehouse para uso departamental. Tanto el DataWarehouse como el Datamart son sistemas orientados a la consulta, en los que se producen procesos batch de carga de datos (altas) con una frecuencia baja y conocida. Ambos son consultados mediante herramientas OLAP (On Line Analytical Processing) que ofrecen una visión multidimensional de la información. Sobre estas bases de datos se pueden construir EIS (Executive Information Systems, Sistemas de Información para Directivos) y DSS (Decision Support Systems, Sistemas de Ayuda a la toma de Decisiones). Por otra parte, se conoce como Data Mining al proceso no trivial de análisis de grandes cantidades de datos con el objetivo de extraer información útil, por ejemplo para realizar clasificaciones o predicciones. A continuación se muestra una representación espacial de una variable multidimensional con una, dos y tres dimensiones. En esta figura los cubitos representan valores de dimensión, y las esferas son datos.
Una variable unidimensional podría ser el cambio de la peseta con el dólar, que sólo varía en la dimensión <tiempo>. Los cubitos serían, por ejemplo, los meses del año y las esferas serían los valores numéricos correspondientes al cambio monetario en cada momento. Un ejemplo de variable de dos dimensiones es el número de habitantes, que se mueve por las dimensiones <Geografía> y <tiempo>. Finalmente, los ingresos de una organización podrían almacenarse mediante una variable de tres dimensiones: <producto>, <Geografía> y <tiempo>. Normalmente los elementos de una dimensión forman una jerarquía, con lo que algunos son padres de otros. Cuando las variables multidimensionales de un datamart o datawarehouse son cargadas con nueva información (por ejemplo, mensualmente a partir de ficheros de texto), ésta se refiere a los nodos hoja del árbol jerárquico de cada una de las dimensiones. Por ejemplo, la información de ventas llega detallada por producto, por provincia y por mes. Pero si queremos obtener el total de ventas de todos los productos, el total de ventas de todas las provincias, el de todos los meses del año, o alguna combinación de estos, deberemos realizar un proceso de agregación de la información. Por ejemplo, en la dimensión Producto incluiremos un valor llamado "Total Productos" que será padre de todos los demás productos y que contendrá el acumulado de todos ellos. En la dimensión tiempo podremos tener, por ejemplo, el año 2000 descompuesto en trimestres, y estos a su vez en meses. La información llega detallada por producto y por mes, y posteriormente a la carga de datos, se realiza un proceso de agregación que calcula estos acumulados. OLAP, R-OLAP y M-OLAPUn sistema OLAP se puede entender como la generalización de un generador de informes. Las aplicaciones informáticas clásicas de consulta, orientadas a la toma de decisiones, deben ser programadas. Atendiendo a las necesidades del usuario, se crea una u otra interfaz. Sin embargo, muchos desarrolladores se dieron cuenta de que estas aplicaciones eran susceptibles de ser generalizadas y servir para casi cualquier necesidad, esto es, para casi cualquier base de datos. Los sistemas OLAP evitan la necesidad de desarrollar interfaces de consulta, y ofrecen un entorno único valido para el análisis de cualquier información histórica, orientado a la toma de decisiones. A cambio, es necesario definir dimensiones, jerarquías y variables, organizando de esta forma los datos. Para los desarrolladores de aplicaciones acostumbrados a trabajar con bases de datos relacionales, el diseño de una base de datos multidimensional puede ser complejo o al menos, extraño. Pero en general, nuestra experiencia nos dice que el diseño de dimensiones y variables es mucho más sencillo e intuitivo que un diseño relacional. Esto es debido a que las dimensiones y variables son reflejo directo de los informes en papel utilizados por la organización. Una vez decidido emplear un entorno de consulta OLAP, se ha de elegir entre R-OLAP y M-OLAP. R-OLAP es la arquitectura de base de datos multidimensional en la que los datos se encuentran almacenados en una base de datos relacional, la cual tiene forma de estrella (también llamada copo de nieve o araña). En R-OLAP, en principio la base de datos sólo almacena información relativa a los datos en detalle, evitando acumulados (evitando redundancia). En un sistema M-OLAP, en cambio, los datos se encuentran almacenados en ficheros con estructura multidimensional, los cuales reservan espacio para todas las combinaciones de todos los posibles valores de todas las dimensiones de cada una de las variables, incluyendo los valores de dimensión que representan acumulados. Es decir, un sistema M-OLAP contiene precalculados (almacenados) los resultados de todas las posibles consultas a la base de datos. M-OLAP consigue consultas muy rápidas a costa de mayores necesidades de almacenamiento, y retardos en las modificaciones (que no deberían producirse salvo excepcionalmente), y largos procesos batch de carga y cálculo de acumulados. En R-OLAP, al contener sólo las combinaciones de valores de dimensión que representan detalle, es decir, al no haber redundancia, el fichero de base de datos es pequeño. Los procesos batch de carga son rápidos (ya que no se requiere agregación), y sin embargo, las consultas pueden ser muy lentas, por lo que se aplica la solución de tener al menos algunas consultas precalculadas. En M-OLAP, el gran tamaño de las variables multidimensionales o el retardo en los procesos batch puede ser un inconveniente. En este documento se proponen algunas soluciones a estos problemas, aplicables en tiempo de diseño de la base de datos. Cálculo del tamaño de una variable multidimensionalEn lo que sigue supondremos que trabajamos con un sistema M-OLAP. Durante el diseño de la base de datos multidimensional, antes de la creación de los objetos, es interesante predecir, para cada una de las variables que se espera utilizar, y cuyo tamaño se supone importante:
Sin tener en cuenta el uso de técnicas de compresión, el tamaño de una variable multidimensional dependerá del número de valores de cada una de las dimensiones por las que "se mueva" la variable, incluyendo los valores acumulados. Dada una variable multidimensional V dimensionada por D1, D2,... Dn V(D1, D2,... Dn) Siendo N[Di] el número de valores de cada dimensión, el número de celdas de la variable multidimensional NC[V] será el producto de estos valores, es decir:
Por ejemplo, dada la variable multidimensional V.Ventas (<Artículo>, <Geografía>, <Tiempo>) Siendo N[<Artículo >] = 10 N[<Geografía>] = 50 N[<Tiempo>] = 20 Podemos calcular el número de celdas de la variable de la forma: NC[V] = N[<Artículo >] * N[<Geografía>] * N[<Tiempo>] = 10 * 50 * 20 = 10000 Para los análisis posteriores nos será de gran utilidad distinguir cuántas de estas celdas representan información acumulada y cuántas representan un detalle. Entendemos como celdas de detalle aquellas que son hojas en todas las dimensiones. Normalmente las variables multidimensionales como V.Ventas y sus dimensiones se definen de forma que las celdas de detalle de la variable puedan ser cargadas mediante la asignación directa de cada una de las líneas de datos contenidas en el fichero de entrada. Un fichero que cargue nuestra variable de ejemplo podría tener el siguiente aspecto:
// Las lineas 1
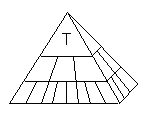
a 5 son de cabecera, y los Cada una de las líneas leídas de este fichero se imputará, en principio, a una celda de detalle. Asignaremos cada dato (el campo Unidades Vendidas) a una celda del cubo de V.Ventas, identificada por un valor de artículo, un valor de geografía y un valor de tiempo. Como ya se ha dicho, las celdas de detalle son aquellas que son hojas en todas las dimensiones. Las celdas de acumulados (o las celdas que no son de detalle) serán aquellas que no son hojas en todas las dimensiones, o lo que es lo mismo, que son celdas de acumulados por al menos una de las dimensiones. Aunque se trabaje con un número de dimensiones mayor que tres, las variables n-dimensionales se suelen representar mediante cubos, ya que estas figuras ofrecen una aproximación intuitiva útil a la n-dimensionalidad. Otra forma de ofrecer una visión intuitiva de las variables multidimensionales, esta vez incidiendo en el aspecto de las jerarquías de las dimensiones, es mediante pirámides.
En esta representación, las caras de la pirámide que no son su base representan dimensiones, destacándose en ellas las jerarquías. Los valores de detalle corresponden con los bloques inferiores, que soportan al resto. Esta analogía tiene el inconveniente de ocultar el hecho de que existen datos indexados por cualquier valor de cualquier dimensión relacionado con cualquier otro de cada una de las demás, y no sólo cada valor de dimensión con los de su mismo nivel jerárquico, como ocurre en la pirámide. Aunque pudiera parecer extraño, existen muchos casos en los que el número de datos calculados mediante agregación es muy superior al de los datos simplemente cargados directamente en la base de datos. Es decir, es posible que el número de celdas de acumulados sea superior al número de celdas de detalle, y tengamos una "pirámide invertida". Si suponemos que cada dimensión tiene una única jerarquía, el número total de valores de una dimensión (Dt) será la suma de los valores que sean padres, es decir, que tengan hijos (Dp) más aquellos que no los tengan y sean por tanto nodos hoja (Dh). En
la primera dimensión Ya que para que una celda se considere detalle, ha de serlo por todas las dimensiones, el número total de celdas de detalle (NCD) de una variable multidimensional será el producto del número de valores hoja de cada dimensión
Podría parecernos que el número total de celdas acumuladas (NCA) sería el producto del número de valores acumulados por cada dimensión, pero esto no es así, ya que basta con que un valor de una dimensión no sea detalle para que todas las celdas referenciadas por ese valor de dimensión tampoco sean detalle. El número total de celdas acumuladas (NCA) lo podemos calcular restando del total de celdas (NC), las que son de detalle (NCD). NC[V] =
NCD[V] + NCA[V] El número de celdas acumuladas (NCA) será mayor que el número de celdas de detalle (NCD) cuando: NCA[V] >
NCD[V] Mediante una combinación de medidas analíticas y estimaciones obtenidas de la experiencia, es posible predecir con suficiente calidad la ocupación de una variable en cuanto a espacio en disco, así como el tiempo requerido para la agregación de los valores de detalle. Ya que el tamaño de las cargas no suele variar mucho
de un mes a otro, es habitual realizar experimentos de carga y agregación
con algún reducido conjunto de valores de la dimensión Una vez que hemos estimado el espacio en disco necesario para el almacenamiento de los datos, y el tiempo requerido para las agregaciones, es posible que estos valores superen los recursos disponibles. A continuación se van a mostrar algunas posibles soluciones a estos problemas, aplicables en tiempo de diseño y en la gran mayoría de casos. Para ello, se aprovecharán algunas particularidades del uso que se hace de estas variables. Cómo reducir el tamaño de una variableLas variables multidimensionales pueden estar comprimidas, por ejemplo, mediante la tecnología sparse de Oracle Express. Sin embargo, es posible que por diversas razones no queramos utilizar una variable comprimida, o que a pesar de utilizar compresión, el espacio ocupado por la variable siga siendo excesivo. Las formas obvias de reducir el tamaño de una variable son eliminar dimensiones y eliminar valores de dimensión. Por ejemplo, si podemos prescindir de un detalle diario, y nos basta la información semanal, podremos ahorrar mucho espacio en disco. Una vez que las dimensiones y valores de dimensión se han reducido al mínimo aceptable, y existiendo aún problemas de espacio, siempre nos queda la opción de eliminar algunos de los valores acumulados de la dimensión, ya que podrán ser calculados a partir de sus hijos. Pero no deberíamos aplicar masivamente esta solución, ya que entorpeceríamos las consultas. Precisamente, las bases de datos multidimensionales pretenden, entre otras cosas, agilizar consultas disponiendo de valores precalculados. Lo más adecuado es aplicar esta técnica en dimensiones pequeñas. Por ejemplo, si la variable posee alguna dimensión con tres valores, uno de ellos total, eliminando el valor total de la dimensión se ahorra un tercio del espacio, y los cálculos realizados bajo demanda suponen sumas de pocos (dos) valores. En cambio, si el número de valores de la dimensión fuese elevado, el ahorro sería mucho menor, y los cálculos más lentos. En realidad podríamos eliminar cualquiera de los tres valores, y ya que el total será probablemente el más consultado tal vez fuera mejor eliminar alguno de los hijos, aunque esto complicaría los programas de carga de datos. Sin embargo, en cualquier caso el ahorro conseguido con este método no es muy grande ¿Podremos obtener ahorros mucho mayores sin perder el detalle en las consultas? La respuesta es, en la mayoría de los casos, sí. Es muy probable que la variable que queremos comprimir tenga un elevado número de dimensiones, y éstas a su vez, muchos valores de dimensión. Si tenemos problemas con el tamaño de la variable, es porque ésta es realmente grande. Ocurre que cuantas más dimensiones y más valores de dimensión tiene una variable, tanto menos probable es que algún usuario desee consultar algún valor de la variable que esté indexado por valores de dimensión hoja en todas sus dimensiones. Recordemos que se trata de sistemas orientados a la toma de decisiones. En una variable de ocho dimensiones será rarísimo querer consultar algún dato que no esté acumulado en al menos una de las ocho dimensiones. Restringiendo un poco más la hipótesis, podríamos suponer que en todas las consultas a la variable, al menos por una de las dimensiones, se va a solicitar el valor acumulado total (el más alto de la jerarquía). A continuación veremos un ejemplo de esto con una variable de tres dimensiones. Esta solución implica el uso de variables y fórmulas multidimensionales. En las bases de datos multidimensionales se almacenan tanto variables como fórmulas. Las variables contienen datos. Las fórmulas en cambio, son expresiones o programas que acceden a variables y/o a otras fórmulas, y que indican la manera de calcular los datos que serán presentados al usuario. Según la solución propuesta, en vez de almacenar una variable del tipo V(D1 D2 D3) Se almacenan tres variables: V1(D1 D2) Cuyas necesidades de espacio serán menores o iguales, siempre que se cumpla que NC[V] >= NC[V1] + NC[V2] + NC[V3] Es decir Dt1 * Dt2 * Dt3 >= Dt1 * Dt2 + Dt1 * Dt3 + Dt2 * Dt3 Siendo esta una condición que se cumple habitualmente. Para el caso que nos ocupa, puede considerarse que se cumple siempre, ya que es condición suficiente (aunque no necesaria) que en cada dimensión existan al menos tantos valores de dimensión como el número total de dimensiones de la variable, es decir, si n es el número de dimensiones y Dti es el número de valores de la dimensión i, basta con que se cumpla:
Se construye una fórmula F1(D1 D2 D3) que dependiendo del total consultado, extraiga los datos de una u otra variable, de la forma: F1 = Utilizando la analogía espacial, en vez de almacenar todo el cubo de datos, se almacenan sólo los datos de las caras del cubo, ya que siempre al menos uno de los ejes (dimensiones) tiene el valor total (que se considera en el eje de coordenadas). Se almacenarán tantas caras de cubo como dimensiones existan, en este caso, sólo tres. Por ejemplo, si el número de valores de cada dimensión fueran 10, 50 y 20 respectivamente, en vez de almacenar los datos en una variable de 10 * 50 * 20 celdas = 10000 celdas, tendríamos tres variables de 10 * 50, 10 * 20 y 50 * 20 celdas, en total, 500 + 200 + 1000 = 1700 celdas. Si obligásemos a que al menos dos dimensiones se consulten como totales, estaríamos almacenando las "aristas" del cubo o hipercubo. Por ejemplo, una variable de cinco dimensiones V(D1 D2 D3 D4 D5) Podría almacenarse en 10 variables, cuyo número corresponde con todas las combinaciones de las dos dimensiones que se consultarán a total:
D1 D2 O desde otro punto de vista, y dado que comb(n, m) = comb(n, n - m) se trata de todas las combinaciones de las tres de esas cinco dimensiones que no estarán a total:
V1(D1 D2 D3) Construyéndose una fórmula F1(D1 D2 D3 D4 D5) F1 = Esta implementación afectaría a los programas de carga, que deberían realizarse de forma que acumulen (y no sólo imputen) cada uno de los datos en todas las variables. Si la variable fuese de dos dimensiones, y obligamos a que al menos una de ellas sea total, tendríamos V(D1 D2) Almacenada mediante V1(D1) V2(D2) Que reduce el espacio ocupado siempre que Dt1 * Dt2 > Dt1 * + Dt2 Y creándose la formula F1(D1 D2) F1 = Podemos aplicar este sistema con cualquier valor de dimensión y no sólo con el valor total, simplemente incluyendo una nueva variable que implícitamente almacene los valores que correspondan con ese valor de dimensión, cuya dimensión será precisamente la que esa variable no posee. Por ejemplo, dada una variable multidimensional de cuatro dimensiones: V(D1 D2 D3 D4) Si la dimensión D2 estuviese formada por un total T que tuviese dos hijos subtotales ST1 y ST2, y restringiéramos las consultas de forma que se suponga que siempre se soliciten datos indexados por al menos un total o subtotal por alguna de las dimensiones, los datos se pueden almacenar en las variables:
V1(D1 D2 D3) Implícitamente supone D4 a T Creándose la fórmula F1(D1 D2 D3 D4) F1 = Cómo reducir el tiempo de las agregacionesEn algunas implementaciones de bases de datos multidimensionales, el tiempo necesario para precalcular todas las posibles agregaciones de una variable multidimensional es excesivo. Aunque hay espacio suficiente para poseerlas todas, no hay tiempo suficiente para calcularlas. Si el numero de agregaciones es excesivo, una solución es no precalcularlas todas, y calcularlas bajo demanda. Es decir, simplemente podemos dejar de agregar en una dimensión, agregando en todas las demás y calcular en esa dimensión únicamente los valores solicitados por el usuario. Por ejemplo, si la dimensión D1 posee cuatro valores que son: T, V1, V2 y V3, siendo T el padre de V1, V2 y V3, una variable cualquiera dimensionada por D1, como por ejemplo V1(D1 D2 D3 D4 D5 D6 D7) podría no necesitar ser agregada por D1 siempre que, en vez de consultar directamente V1, se consultase una fórmula F1 que calculase sobre la marcha el acumulado T en caso de solicitarse, es decir: F1 = Si la estructura de la jerarquía fuese más compleja, la fórmula quedaría más compacta haciéndola recursiva. Por ejemplo, si T tuviese dos hijos subtotales ST1 y ST2 los cuales a su vez, tuvieran los hijos, por una parte, ST1A, y ST1B y por otra ST2A, ST2B, y ST2C respectivamente, el total de la fórmula podría calcularse a partir de los subtotales: F1 = Podríamos aplicar este método por más de una dimensión. Por ejemplo, si en la variable V1(D1 D2 D3 D4 D5 D6 D7) quisiéramos realizar bajo demanda las agregaciones por D1 y D2, bastaría con agregar por el resto de dimensiones y crear dos fórmulas como F1 y F2, consultando F2 en vez de V1. F1 = F2 = F2 realiza bajo demanda las agregaciones en D2 y para ello consulta F1, que es quien agrega D1 leyendo de V1. El principal problema de esta solución es que las modificaciones de la dimensión deberán reflejarse en estas fórmulas. Para facilitar este trabajo, puede ser muy útil construir un programa que recorra la estructura jerárquica de la dimensión y genere el texto de la fórmula que refleja las relaciones entre valores. Resumiendo, si el tamaño de una variable es excesivo, podemos reducirlo descomponiendo la variable en otras a las cuales le falte alguna de las dimensiones, consultando una fórmula que extraiga cada vez la información de la variable correspondiente. Si las agregaciones son lentas, podemos no agregar por todas las dimensiones y calcular bajo demanda las agregaciones restantes. En este caso, es interesante que la dimensión excluida de la agregación sea grande. Referencias
Páginas en InternetOracle
Microstrategy Business Objects OLAP
Data Warehouse
Datamining
|