Se abordan en este capítulo una serie de estudios sobre características de ECGI que se han decidido analizar empíricamente, ya sea porque su estudio teórico era excesivamente complejo, ya sea porque eran cuestiones cuya respuesta sólo tenía sentido en el contexto de una aplicación práctica:
* Variación en el comportamiento de ECGI en función del
criterio de disimilitud utilizado.
* Convergencia de ECGI.
* Ambigüedad de las gramáticas generadas por ECGI.
* Necesidad o no de incluir las reglas de inserción y borrado en la
fase de reconocimiento de ECGI.
* Importancia relativa de la información aportada por las distintas
estadísticas que que utiliza ECGI estocástico (frecuencia de las
reglas, de los errores, de ambas).
Resulta difícil establecer en principio cuál de los criterios definidos en el capítulo 6.6 (minE: minimizar errores, minEL: minizar errores respecto a la longitud de la derivación y maxA: maximizar aciertos) es el más adecuado para ECGI en el caso más general.
Por otra parte, la comprobación experimental demuestra que los resultados de reconocimiento de ECGI no se ven afectados drásticamente por un cambio del criterio utilizado, por lo menos en los problemas aquí tratados.
Cada línea de la tabla que se muestra a continuación (tabla 9.1), corresponde a la utilización de ECGI con uno de los tres criterios estudiados en el capítulo 6. Cada línea corresponde a la aplicación de uno de los criterios al conjunto de experimentos de reconocimiento de dígitos manuscritos con resolución de rejilla 6 descrito en el capítulo 8. Como ya se explicó en dicho capítulo, cada experimento es en realidad un conjunto de 12 experimentos en los que se hallan involucrados un total de 120 autómatas (10 por experimento) y en los que se han llevado a cabo 48000 análisis sintácticos (400 muestras se han presentado a cada autómata). En el reconocimiento se ha utilizado el modelo de error restringido a solo sustituciones (capítulo 6 y 7).
Min..Max : Med Peor..Mejor : Med
maxA 223 3,71 1,8.1040 11..145 : 69 95..99.75 : 98.15
minEL 271 2,37 1,7.1034 16..145 : 68 93..99.75 : 97.71
minE 475 1,94 2,2.1032 20..140 : 70 94..99.75 : 98.15
En la tabla se muestra el promedio del número de estados inferidos, del factor de ramificación (Factor de Ramificación: número de reglas con el mismo no terminal a la izquierda) y del número de cadenas de los lenguajes inferidos. Asimismo se muestra la longitud mínima, máxima y promedio de las cadenas de esos mismos lenguajes; finalmente, el % de cadenas correctamente reconocidas en el peor, mejor y en promedio de los 12 experimentos.
Los resultados, tal como sugería la discusión teórica del capítulo 6, se inclinan a favor de maximizar el número de aciertos. Se comprueba que la diferencia, en lo que se refiere a resultados de reconocimiento, es pequeña comparada con minEL (0.44%), pero a favor de maxA. MaxA mejora de un 2% el peor de los casos, no empeorando el mejor. Además, maxA proporciona automatas con un 18% menos de estados que minEL, aunque eso sí, con mayor número de reglas (22% más) debido a un mayor factor de ramificación.
Es muy notable el que la minimización de errores sin normalización proporcione los mismos resultados de reconocimiento que maxA, pero generando automatas con un 100% más de estados (y un 10% más de reglas). Esta es la razón por la que este criterio no se haya utilizado en la práctica.
No cabe sin embargo afirmar que maxA proporcione siempre resultados mejores, aunque en general los mejora más que los empeora. Otro experimento de comparación de distancias se llevó a cabo repitiendo el reconocimiento en el peor (R6) y el mejor (R1) de los 12 casos (R1 a R12) del experimento anterior, pero esta vez utilizando un modelo de error completo en reconocimiento (tabla 9.2).
R6 R1 R6 R1
maxA 95 99,75 95.75 99.00
minEN 93 99,75 94.25 99.75
Aquí maxA proporciona en R1 resultados 0.75% peores, posiblemente debido a que, al producir un lenguaje mucho mayor (6 órdenes de magnitud), generaliza demasiado al superponer a las gramáticas el modelo de error completo, lo cual por otro lado es una ventaja si el aprendizaje es insuficiente (R6).
Para comprobar si la eficacia relativa de los distintos criterios dependía del problema abordado se repitió el experimento HLKO11 (dígitos hablados, ver capítulo 8), utilizando las tres distancias, también con el algoritmo estocástico de reconocimiento, pero una vez con modelo de error completo y otra prohibiendo inserciones y borrados. Aquí cada entrada de la tabla corresponde a 10000 análisis sintácticos (5 experimentos con 10 autómatas, 200 muestras presentadas a cada autómata) (tabla 9.3).
En el caso de los dígitos hablados, la tasa de reconocimiento se inclina ligeramente a favor de minEL, probablemente porque se requiere mayor generalización al haber mayor variabilidad en los datos.
Por otra parte, la consideración de la ambigüedad de las gramáticas generadas, también puede hacer dudar a la hora de elegir el criterio más conveniente (ver más adelante).
Peor..Mejo : Med
maxA 171 2,53 1,3.1018
Reconocimiento con Modelo de Error Completo 99..100 : 99,6
Reconocimiento con Sólo Substituciones. 99..100 : 99,7
minEN 197 1,97 6,2.1014
Reconocimiento con Modelo de Error Completo 99,5..100 : 99,8
Reconocimiento con Sólo Substituciones. 99,5..100 : 99,8
minE 246 1,79 3,3.1013
Reconocimiento con Modelo de Error Completo 98,5..100 : 99,6
Reconocimiento con Sólo Substituciones. 98,5..100 : 99,2
De la propia definición de ECGI se observa que sólo se añaden reglas (y no terminales) cuando se produce la aparición de una (sub)cadena aún no modelizada (en esa posición) por la gramática inferida. De ello se deduce inmediatamente que el tamaño de la gramática inferida por ECGI no está limitado a priori, pues siempre es posible que aparezca una (sub)cadena no modelizada aún por la gramática.
Sin embargo, podemos asumir que todo conjunto de muestras real tiene una variabilidad limitada, puesto que, por hipótesis, pertenece al lenguaje de una gramática inferible. Es por lo tanto lícito suponer que, si ECGI es un método adecuado de inferencia para esa gramática, llegará un momento, en que ECGI no tenga que añadir prácticamente ningún estado más, al contener la gramática construída a la buscada. A ello puede contribuir además, el hecho empírico de que el tamaño del lenguaje inferido crece exponencialmente con el número de reglas añadidas
El problema de la convergencia del aprendizaje realizado por ECGI se presenta entonces más bien como el problema de determinar lo apropiados que son los heurísticos de ECGI para una tarea concreta.
El límite máximo de crecimiento de una gramática generada por ECGI viene dado por la inferencia de la gramática canónica de R+, que ECGI generará en el caso (casi imposible) de que todas las (sub)cadenas muestra fueran totalmente dispares en posición y semejanza. En el caso más real, de que la muestra sea muy inadecuada -p.e: proveniente de una gramática con muchos circuitos- ECGI puede no converger y hacer crecer la gramática con un incremento constante determinado por la variabilidad de R+. Recuérdese además que, debido a que no genera circuitos, ECGI no puede inferir gramáticas con cadenas de longitud arbitrariamente largas, y que en todos los casos el número mínimo de estados que genera es igual al de la cadena más larga de R+.
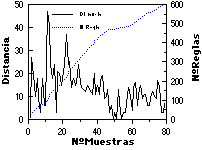
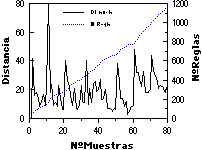
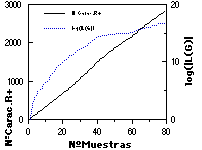
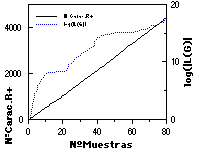
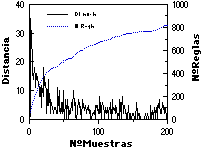
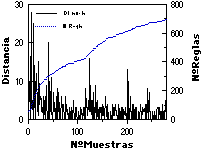
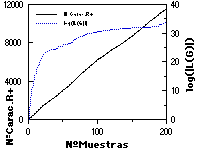
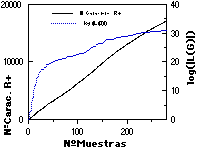
En un caso de aplicación práctica, adecuada a ECGI, se espera que la distancia de las nuevas muestras a la gramática inferida (y por lo tanto el crecimiento de ésta) se irá reduciendo con el número de muestras presentadas, tendiendo asintóticamente hacia un tamaño máximo. Esto se ha comprobado empíricamente en múltiples experimentos (todos los realizados hasta el momento con ECGI), y queda evidenciado en las figuras adjuntas (figuras 9.1 y 9.2), en las que se muestra la distancia de cada nueva muestra a la gramática en ese momento, junto con el número de reglas de la gramática. Obsérvese cómo en algunos casos aprarecen "picos" de variabilidad en el conjunto de muestras (especialmente claros en los dígitos impresos, en las que se cambia de tipo de letra cada 40 muestras), y como en otros se ha detenido la inferencia relativamente lejos de la asíntota (las letras habladas, dada su gran variabilidad).
Asimismo, en la parte inferior de las figuras se muestra 1) el número total de símbolos presentados a ECGI, o número de caracteres total de R+ (que es equivalente al número de reglas de la gramática canónica; comparar con el número de reglas en la parte superior); y 2) la evolución del tamaño del lenguaje de la gramática (con el fin de cuantificar la amplitud de la generalización efectuada por el ECGI), ambas cantidades frente al número de muestras de aprendizaje.
La convergencia de ECGI puede llegar a ser extremadamente rápida, principalmente debido a que el lenguaje de la gramática inferida tiende a crecer exponencialmente (en paralelo con el número de posibles combinaciones de un número cada vez mayor de subcadenas incluídas). Ello, en un caso favorable le hace superar enseguida la posible variabilidad de las muestras. Ello permite a ECGI construir gramáticas muy compactas (un número de reglas un orden de magnitud inferior a la canónica, con 200 muestras) y de hecho, aún reducibles de hasta un 30% sin merma apreciable de resultados (ver la simplificación de autómatas, en capítulo 10).
Como demostración empírica de la compacidad de las gramáticas generadas por ECGI, se adjunta una tabla, correspondiente a la mayoría de los experimentos presentados con detalle en el capítulo 8 (tabla 9.3). Nótese que esta tabla es tan sólo un resumen de resultados ya presentados en dicho capítulo.


Cadenas Autómata Factor G. Canónica
Dígitos Hablados (Muestras/autómata 80)
HLKO11 28,3 196 1,97 1/5,8 6,25.1014
Letras Habladas (Muestras/autómata: 80)
LLKO 56,8 785 1,62 1/4,5 1,2.1026
Dígitos Manuscritos (Muestras/autómata: 200)
Rej4 73,1 310 3,78 1/12.,5 5,6.1070
Rej6 48,1 223 3,71 1/11,6 1,8.1040
Rej8 35,7 175 3,70 1/11 1,1.1031
Rej10 28,3 144 3,60 1/10,8 8,5.1023
Dígitos Impresos (Muestras/autómata: 140)
Rej4 72,82 255 3,57 1/11,2 3,3.1045
Rej6 47,95 174 3,46 1/11,1 1,2.1036
Rej8 35,52 134 3,34 1/11 5,4.1026
Rej10 28,13 114 3,22 1/10,6 6,2.1020
Obsérvese como, cuando hay un número mayor de cadenas de aprendizaje, la diferencia con la gramática canónica aumenta (de 1/5 con 80 muestras, pasa a 1/11 con 200), muestra evidente de la convergencia de ECGI.
Las gramáticas inferidas por ECGI son en general ambiguas, lo cual es poco deseable y, como se vió en el capítulo 7, presenta (entre otros) inconvenientes mayores para una estimación correcta de probabilidades en la extensión estocástica de ECGI.
Para comprobar hasta qué punto es importante la ambigüedad de las gramáticas que genera ECGI, se ha llevado a cabo una comprobación sistemática de (la mayoría) de los autómatas que se generaron en los distintos experimentos.
Dada la no existencia en la literatura de un algoritmo de complejidad aceptable para determinar con estrictamente la no ambigüedad de una gramática no determinista, se procedió a utilizar un método que permite asegurar que la gramática es ambigua, e incluso si es "poco" o "muy" ambigua (es ambigua para relativamente pocas o muchas cadenas).
El método se basa en la comprobación de la existencia de más de un camino de derivación para cada una de las cadenas de un conjunto de muestras dado. Para ello se realiza un análisis sintáctico no determinista (Viterbi) y se detecta cuando dos derivaciones de la misma cadena llegan al mismo no terminal (vértice del trellis). Denominaremos punto de ambigüedad a aquellos vértices del trellis en los que se produzca esta situación.
La siguiente tabla da cuenta de los resultados obtenidos, utilizando como muestras las mismas que sirvieron de aprendizaje a cada autómata (tabla 9.4).
Ambigüedad
Dígitos Hablados (Muestras/autómata 80)
HLKO11 6,39 387 6,25.1014
Letras Habladas (Muestras/autómata: 80)
LLKO 7,55 1272 1,2.1026
Dígitos Manuscritos (Muestras/autómata: 200)
Rej4 353.9 1170 5,6.1070
Rej6 164 826 1,8.1040
Rej8 96,3 649 1,1.1031
Rej10 58,34 519 8,5.1023
Dígitos Impresos (Muestras/autómata: 140)
Rej4 331,13 910 3,3.1045
Rej6 136,8 602 1,2.1036
Rej8 70,10 449 5,4.1026
Rej10 43,31 369 6,2.1020
No se ha encontrado ningún autómata que, habiendo sido generado por ECGI, no sea ambiguo.
El número de puntos de ambigüedad crece con la complejidad de la gramática, lo cual no es del todo inesperado. Nótese que el número de puntos de ambigüedad no es el número de derivaciones posibles de una misma cadena; estas están relacionadas con el número de puntos de ambigüedad de la misma manera que el número de cadenas del lenguaje con el de estados; es decir, de una forma que puede llegar a ser exponencial.
Obsérvese también que la relación del número de reglas con el número de puntos de ambigüedad es muy superior en el caso de reconocimiento de palabras (60 en vez de unos 5 -varía de 3 a 9-). La razón de esto se halla en el criterio de (di)similitud utilizado. En efecto, se comprobó la ambigüedad en un experimento realizado con los distintos criterios (Dígitos manuscritos, rejilla 6) (tabla 9.4).
Ambigüedad Ramificación
Dígitos Manuscritos, rejilla 6. (Muestras/autómata: 200)
maxA 164 223 3,71 826 1,8.1040
minEL 31 270 2,37 642 1,7.1034
minE 20 476 1,9 921 2,2.1032
Sorprendentemente, la distancia maxA proporciona autómatas enormemente más ambiguos, posiblemente debido a que para generar un lenguaje de igual tamaño emplea la mitad de estados, y por consiguiente un factor de ramificación doble. Desde el punto de vista de la ambigüedad, el mejor compromiso es entonces minEL, aunque ya hemos visto que a veces proporciona resultados de reconocimiento inferiores.
Por otra parte, hay que notar que cuando se compararon los criterios maxA y minE, la efectividad de reconocimiento de ambos resultó equivalente, a pesar del hecho de que se estaba utilizando la extensión estocástica, y de que la precisión de la estimación de probabilidades de minE debió ser mucho mayor al ser la gramática mucho menos ambigüa. No parece por lo tanto que, en la práctica, la imprecisa estimación de las reglas afecte mucho a la eficacia de reconocimiento de ECGI. Esto se ve confirmado por los experimentos dedicados a generar autómatas deterministas (capítulo 11) y por otros trabajos que intentaron, mediante reestimación de probabilidades (reconsiderando sucesivas veces el conjunto de muestras), mejorar la eficacia de ECGI; objetivo que no fue alcanzado plenamente [Castaño,90].
En el capítulo 6 se introdujo la posibilidad de reducir la complejidad temporal del análisis sintáctico realizado por ECGI a cada muestra, mediante simplificación del modelo de corrección de errores utilizado. Como se comentó entonces, dicha simplificación consite en prohibir los errores de inserción y borrado, permitiendo tan sólo los de sustitución. Ello no sólo reduce el número de reglas a considerar durante el análisis, sino que permite aplicar diversas técnicas que limitando el número de vértices del trellis visitados, permiten reducir hasta en un 90% la complejidad temporal [Torró,90].
Para comprobar hasta qué punto esta simplificación afecta a los resultados de reconocimiento, no queda más remedio que recurrir a la comprobación empírica. Esta se ha llevado sistemáticamente a cabo en todos los experimentos realizados y descritos previamente en el capítulo 8.
Tanto cuando se utiliza un modelo estocástico (ver capítulo 7) como cuando no, es posible observar que se produce un (pequeño) deterioro de los resultados al prohibir inserciones y borrados. Aunque, en algunos casos, se llega a perder hasta un 3,6%, normalmente se registra, o ninguna pérdida en la tasa de reconocimiento, o bien pérdidas y mejoras del orden de 0.3%, con cierto predominio de las pérdidas (aunque en un caso se ha obtenido hasta un 1% de mejora). Todo esto se resume en la tabla comparativa que se presenta a continuación (tabla 9.5) (solo se presentan los experimentos más significativos, ya que esta tabla es un resumen de resultados ya presentados en el capítulo 8).
No Estocástico
Piloto 98.0 97.0 -1.0
H5 98.5 99.5 +1.0
Estocástico
H1 95.6 99.2 -3.6
HLKO11 99.8 99.8 0.0
Dígitos Manuscritos
Rej4 8.1 98.4 -0.3
Rej6 8.1 98.3 -0.2
Rej8 6.9 96.9 0.0
Rej10 6.3 96.1 +0.2
Dígitos Impresos
Rej4 100 99.9 +0.1
Rej6 99.3 99.7 -0.4
Rej8 99.3 99.4 -0.1
Rej10 97.8 98.5 +0.3
En los casos en los que se midió el tiempo (todos los experimentos de dígitos manuscritos e impresos) se pudo observar, como previsto (al reducirse de un tercio el número de reglas a examinar: de 3.|V|+1 a 2.|V|+1), una reducción sistemática del orden de un 30% en el tiempo de reconocimiento (tabla 9.6).
Dígitos Manuscritos (HP 9380)
Rej4 17 21 36
Rej6 8 10 17
Rej8 5 6 10
Rej10 3 4 6
Dígitos Impresos (RS-6530H)
Rej4 6.22 5.56 8.62
Rej6 2.90 2.60 4.03
Rej8 1.72 1.53 2.33
Rej10 1.17 1.05 1.58
Resumiendo la discusión, se puede afirmar que, en los casos de que sea importante el tiempo de reconocimiento (p.e. tiempo real), se puede recurrir al modelo de error con sólo sustituciones, con una pérdida mínima de eficacia.
En los resultados presentados en el capítulo 8 (algunos de los cuales se resumen en la tabla 9.7) se evidenció la gran importancia que tiene, para las prestaciones en reconocimiento de ECGI, la información estadística incorporada en la extensión estocástica (capítulo 7). Concretamente, y como se puede comprobar en la tabla 9.7, añadir la información probabilística a las reglas mejora a veces de hasta un 7% la tasa de reconocimiento.
No Estocástico Estocástico No Estocástico Estocástico
Dígitos Hablados
Piloto 97,5 99,5 96,5 99,5
H5 99,5 100 98,5 99,75
H6 99,5 100 99 99,8
HLKO11 99,5 99,8 99,5 99,8
Dígitos Manuscritos
Rej4 92,3 98,4 92,5 98,0
Rej6 92 98,3 92 98,1
Rej8 91 96,9 91 96,9
Rej10 89 96 89,4 96,3
La extensión estocástica de ECGI no supone un aumento notable en la complejidad del reconocimiento. El trellis a calcular es idéntico, añadiéndose únicamente una suma y un acceso a tabla en cada punto del mismo (de hecho ello es menos costoso que una normalización subóptima por la longitud del camino). Sin embargo, en vistas a una posible utilización a tiempo real y con en el fin de tener una mejor comprensión del algoritmo, resulta interesante localizar la contribución aportada por cada elemento de la extensión estocástica, y estudiar hasta que punto afectaría a los resultados si se la ignorara. Dos son las simplifaciones que se consideran en los siguientes apartados:
* Ignorar las frecuencias de las reglas de la gramática no
expandida.
* Ignorar las frecuencias de los errores en el modelo de error.
La cantidad de información aportada por las probabilidades P(r) de las reglas (transiciones) se puede estudiar con sólo ignorarlas en el reconocimiento. Para ello, basta obtener las probabilidades de los errores como es normal para ECGI, y generar unas probabilidades ficticias para las reglas que den igual importancia relativa a todas las reglas asociadas a un no terminal.
Sea rk=A->xkBk k=1..m las m reglas asociadas a A[propersubset]N. Un conjunto de probabilidades para dichas reglas p(rk) que da igual importancia a cada una de ellas y asegura la consistencia de la gramática carácterística viene dado por:
Ignorando frecuencia
de las reglas de los errores
L11 76,1 72,2 76,7 77,7
L22 73,8 73,9 77,2 76,1
L33 71,1 72,2 70 76,6
L44 68,3 67,8 70 72,2
L55 60 62,2 62,8 66,6
Media 69,9 69,8 71,3 73,8
Aplicando la misma filosofía que en el apartado anterior, es posible anular la información estadística aportada por el modelo de error y observar las consecuencias. Para ello, una vez estimadas las probabilidades de la gramática característica de la forma usual, es necesario sintetizar una tabla de substitución Tls (ver capítulo 7) que dé una misma importancia a todos los errores de sustitución, a todos los de borrado y a todos los de inserción, determinando de alguna manera la importancia relativa no error/ substitución/ inserción/ borrado.
El heurístico utilizado para obtener los resultados que se muestran en la tabla 9.8, consistió en definir arbitrariamente, para cada símbolo a[propersubset]V, la probabilidad de no error ps(a|a) como 0.5 y repartir el resto de la probabilidad entre la sustitución ps(b|a) (por otro símbolo b[propersubset]V) y el borrado pb(a). A la inserción pi(b) se le da la misma probabilidad que a los otros errores.
También para este caso los experimentos muestran que la tasa de reconocimiento empeora de hasta un 6% al ignorar la información sobre las frecuencias de los errores.