En este capítulo se exponen con detalle los experimentos de reconocimiento de formas que se han realizado a lo largo de este trabajo para comprobar la viabilidad y buen funcionamiento del algoritmo ECGI, así como de sus extensiones.
En primer lugar se describen los conjuntos de datos a partir de los cuales se organizaron los experimentos. Seguidamente, se detallan éstos y se tabulan sus resultados.
En este capítulo no se incluyen los resultados de los experimentos de obtención de cadena media, de simplificación de autómatas, de obtención de autómatas deterministas y de comparación entre los distintos criterios, todos los cuales se hallan a continuación, en los capítulos correspondientes (capítulos 9, 10 y 11). Tampoco se pretende exponer todos los experimentos realizados, pues se han realizado muchos que luego han quedado obsoletos por mejoras (a veces mínimas) en la parametrización, se han visto incluídos en otros por ampliación del conjunto de datos, etc.; sin contar la gran cantidad de pequeñas pruebas que requiere la puesta a punto de un método heurístico como lo es ECGI.
Se han empleado cinco grupos distintos de datos, cada uno de ellos correspondiente a un grupo distinto de experimentos.
De los cuatro grupo de experimentos, dos involucraron dígitos hablados, uno letras habladas y otros dos utilizaron imágenes. De estos últimos el primer grupo correspondía a dígitos manuscritos y el otro a dígitos impresos. El primer grupo de datos de dígitos hablados, basado en una parametrización y etiquetados elementales, se utilizó como experimento piloto cada vez que se desarrollaba un nuevo prototipo de ECGI, pues representaba un auténtico desafío por lo poco elaborado de los símbolos utilizados. Sin embargo, el corpus de datos de letras habladas es, con margen, el más difícil (sobre todo el subconjunto de EE-letras), dada la extrema similitud de las formas a reconocer.
Casi todos los experimentos se realizaron en un ordenador Hewlett-Packard HP9300, con sistema operativo UNIX (HP-UX)[1].
Se describen a continuación los experimentos realizados en el campo para el cual fue diseñado ECGI en un principio: el reconocimiento del habla. Se presentan primero los corpus de datos (el piloto, el principal y las letras), seguidos de la descripcción de los distintos experimentos y de los resultados obtenidos en cada caso.
Los corpora de los dígitos hablados están formados por la pronunciación repetida frente a un micrófono, por parte de uno o varios locutores (según el corpus), de los diez dígitos castellanos (tabla 8.1).
cero /[theta]éro/ 2
uno /úno/ 2
dos /dós/ 1
tres /trés/ 1
cuatro /kwátro/ 2
cinco /[theta]ínko/ 2
seis /ses/ 1
siete /sjete/ 2
ocho /óco/ 2
nueve /nwé[beta]e/ 2
El corpus de las letras habladas está formado por las treinta letras del alfabeto castellano (tabla 8.2).
B /be/ K /ka/ RR /ée/
C /[theta]e/ L /éle/ S /ése/
CH /ce/ LL /é[lambda]e/ T /te/
D /de/ M /éme/ U /u/
E /e/ N /éne/ V /ú[beta]e/
F /éfe/ Ñ /é[eta]e/ W /ú[beta]edóble/
G /xé/ O /o/ X /ékis/
H /áce/ P /pe/ Y /ígrié[gamma]a/
I /i/ Q /ku/ Z /[theta]éta/
Llamaremos "EE-letras" al conjunto de 9 letras {F, L, LL, M, N, Ñ, R, RR, S} cuya pronunciación se diferencia estrictamente por la consonante intermedia (no confundir con las E-letras {B,C,D,E,G,P,T y -en inglés- V y Z}, que se diferencian por la consonante inicial).
Las palabras fueron adquiridas en una habitación no especiamente aislada, mediante un micrófono de proximidad (relación señal/ruido ~ 40 dB). Se trata de experimentos de reconocimiento de palabras aisladas, por lo que existía una gran pausa entre palabra y palabra, con el fin de trivializar su extracción y segmentación del fondo. El proceso de conversión de estas palabras en cadenas de símbolos es distinto para cada uno de los corpora presentados, aunque sigue el esquema adquisición, parametrización y etiquetado presentado en el capítulo 1.
El grupo de datos que conforman el corpus piloto fué adquirido y cuantificado linealmente mediante un conversor A/D de 12 bits a una frecuencia de muestreo de 8533 Hz.
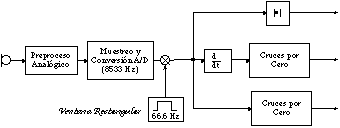
Cada palabra adquirida se sometió posteriormente a un submuestreo en el que se aplicó una ventana rectangular de longitud 256 muestras (20 mseg.) con una frecuencia de 66.6 Hz.. De cada ventana se extrajeron tres parámetros muy elementales: la amplitud media, la densidad de cruces por cero y la densidad de cruces por cero de la primera derivada de la señal (preénfasis) (ver [Casacuberta,87] para una descripción mas completa de estos parámetros), que permiten detectar con cierta seguridad segmentos fricativos y realizar una clasificación "tosca" de las vocales (figura 8.1).

U Vocal posterior
N Sonora débil
S Fricativa fuerte
Z Fricativa débil
T Oclusiva.
Cada ventana, descrita por estos tres parámetros se sometió a un procedimiento de etiquetado difuso (descrito en [Vidal,85]), para luego asignarle el símbolo de la etiqueta difusa más evidente, o el símbolo "?" si ninguna era los suficientemente evidente.
Un único locutor pronunció (en varias sesiones) 58 repeticiones de cada uno de los dígitos. El corpus se compone por lo tanto de un total de 580 cadenas, habiendo resultado la longitud media de las mismas ser 43 caracteres (figura 8.2).
/CERO/ ZZZZZZIIIIIIIZIIIUUUIN??ZZTZZ
/UNO/ ZUUUUUUUN?NNIUUIIINNN?ZZZZ
/DOS/ ZIIIUUIUUUIISSSSSSSSSSZ
/TRES/ NIINIIIIIIIIIUINSSSSSSSSSSSSZ
/CUATRO/ ZZZUUUUUUUU?TTZNIIZ?NUUUNN??Z
/CINCO/ ZZZZZZZ?II?NNNNNNN?TTT?ZIUIUUUINNN?ZZZZ
/SEIS/ ?SSSSSSS?IIIIIIIIIIIIIN?SSSSSSSSSSS
/SIETE/ ZSSSSSSSZIIIIIIIITTTTTZIIIIINNN?Z??
/OCHO/ ZZZ?IIUUUITTTTSSSSSIIIIIINNN?ZZZZ
/NUEVE/ ZZNNIIUUUUUUUUUUIIIINN?SZZZZ
El grupo de datos que conforman el corpus principal fue adquirido y cuantificado linealmente mediante un conversor A/D de 12 bits a una frecuencia de muestreo de 8533 Hz.
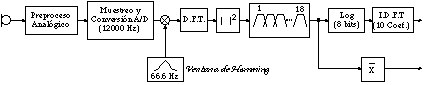
Cada palabra adquirida se sometió posteriormente a un submuestreo en el que se aplicó una ventana de Hamming [Casacuberta,87] de 30 msg. (128 muestras) con una frecuencia de 66.6 Hz. (128 muestras). De cada ventana se extrajeron 11 parámetros, 10 de ellos correspondían a 10 coeficientes cepstrales y el undécimo a la energía media en la ventana (convenientemente normalizada). En [Benedí,89] se dan los detalles del procedimiento para calcular los coeficientes cepstrales, que se resume en (figura 8.3):
* Obtención de la transformada (rápida) de Fourier,
que proporciona 128 puntos complejos correspondientes a las frecuencias de 0 a
4267 Hz.
* Obtención del módulo de la transformada, elevando al
cuadrado dichos valores complejos.
* Submuestreo frecuencial, mediante aplicación de 18 ventanas
trapezoidales distribuídas según la escala de Mel[2].
* Codificación de cada uno de los 18 valores de este banco de
filtros, a 8 bits con escala logarítmica.
* Análisis cepstral de estos 18 valores, es decir
aplicación a ellos de una tranformada inversa de Fourier. La
información contenida en cada uno de los 18 coeficientes así
obtenidos decrece con su índice, reteniéndose los más
significativos para el problema concreto: en nuestro caso los 10 coeficientes
cepstrales.
El conjunto de vectores para el agrupamiento estaba constituído por 4171 vectores extraídos de 150 palabras, las cuales corresponden a las primeras 5 repeticiones de cada dígito, pronunciadas por 3 de los locutores, 1 femenino y 2 masculinos (locutores 1,7,8). Estos locutores se escogieron porque no aparecían en las muestras de test y sí en las de aprendizaje en la mayoría de los experimentos.
Once locutores pronunciaron, en varias sesiones, 10 repeticiones de cada uno de los dígitos castellanos. El corpus se compone pues de un total de 1100 palabras, que se distribuyeron de distintas maneras para realizar los experimentos. La longitud media de las cadenas es de 28,3 caracteres (figura 8.4).
/CERO/ TZZZZZvEEEEEEEErZEEvvoooUUT
/UNO/ UUUUUUUooNNNNvvvoooUUUUT
/DOS/ ZvvOOOOOOOvvvSSSSSSSSSSSSST
/TRES/ ZrEErrEEEeveeeenrSSSSS
/CUATRO/ UUoUUOOOOOvNTTTZZZSZSZvooUUnTTT
/CINCO/ TZZreIIIIINNNNNNnTTTKToooooUUTTT
/SEIS/ SSSSSSSZrvEEEEEeeeIIInnnrSSSSS
/SIETE/ SSSSSSrIIIIEEEenTTTTZZeeeennTTT
/OCHO/ ToOOOOOvvTTTTZZSSSSevvUUUUTTT
/NUEVE/ TnNNvEOOvEEEEEvNNeeeeennnnnTT
La parametrización para el corpus de letras siguió un procedimiento similar al de los dígitos (corpus principal), si se exceptúa la utilización de una frecuencia de muestreo mayor (133.3 Hz.), para disponer de una mayor finura de análisis de fonemas individuales (con una frecuencia de submuestreo de 66.6 Hz. es muy posible que una transición quede representada por un único símbolo), y un clustering que proporciona 32 símbolos en lugar de 15; estando todos estos cambios justificados por la mucho mayor dificultad de la tarea de reconocimiento planteada.
/F/ uUooJJJJJJJJJJJeeeMVUUUUUUUUUUUUUUVeeeeooooeIIIAAAAAA
/L/ UoJJJJJJJJJJJJJJJMRRReTTVTVMMoooooooooIIIAAAAAuu
/LL/ UoJJJoeoooooooooMMVVVVVMMeMMMMoooooooooooooIIIAAAA
/M/ uUoJJJJJJJJJJJJJJJeeeVVVVVVEEeJoooooIIIIIIAAAAA
/N/ UoJJJJJJJoJJJooooeeIIISSSIIIIoooooooooooooIIIIAAAA
/Ñ/ uUoJJJJJJJJJJJooooeIIIIIIIIIIIIIZZFFIIIGGGGGoIIIIIAAAAA
/R/ KoJJJJJJJJoeJJJJJJJJoeVUUooooooooooooooIIIAAAuuuuuuu
/RR/ UJJJJJJJJJJJJJJJJJJJNNEXENNEENSSSSSEEEeeoeeeeIIIAAAAAuuuur
/S/ uIooJJJJJJJJJJJJeeMGHHHHHHHHHHHHHHHHPIIeeeeeIIIIIAA
Para cada corpus se realizaron una serie de experimentos, ya partiéndolo de distintas maneras en conjuntos de aprendizaje y test, ya utilizando distintas variantes de ECGI (no estocástico, estocástico, sólo autorizando sustituciones: capítulo 7). Las variantes <<Ignorando las frecuencias de los errores>> e <<ignorando las frecuencias de las reglas>> se describen con detalle en el capítulo 9.
En todos los experimentos realizados con el corpus piloto se utilizaron las 38 primeras muestras de cada dígito como conjunto de aprendizaje, y las 20 siguientes como muestras de test. Los autómatas se infirieron con lel criterio minEL (ver apartado 6.6). Las tasas de reconocimiento de los experimentos efectuados, variando el tipo de algoritmo de reconocimiento fueron las mostradas en la tabla 8.4 (cada experimento implica el reconocimiento de 200 muestras).
| Algoritmo
de Reconocimiento
|
%Aciertos
|
| No
estocástico
|
|
| Modelo
de error completo
|
97,5
|
| Sólo
substituciones
|
96,5
|
| Estocástico
|
|
| Modelo
de error completo
|
99,5
|
| Ignorando
frecuencia de los errores
|
98,5
|
| Sólo
substituciones
|
99,5
|
| Sólo
substituciones, ignorando frecuencia de las reglas
|
99,5 |
| Sólo
substituciones, ignorando frecuencia de los errores
|
99 |
| Número
medio de estados
|
1063
|
En un apéndice se dan el tamaño de cada uno de los autómatas inferidos, que varía de 73 a 136 estados.
Como ejemplo visual de cómo distintos modelos representan realmente distintas estructuras, se adjunta la figura 8.6 con los 10 autómatas inferidos en con este corpus de datos.
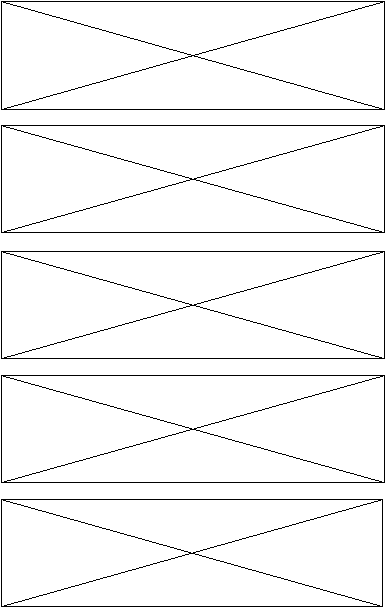
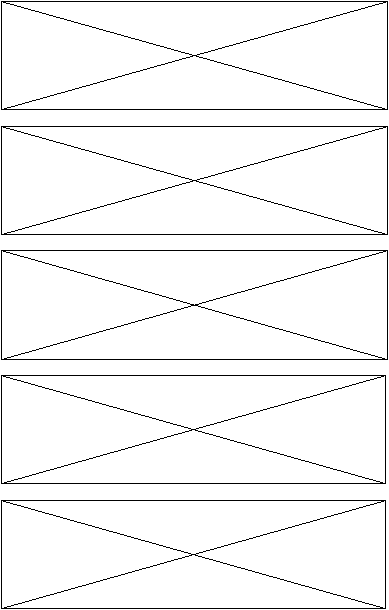
Figura 8.6 (b) Los 10 autómatas inferidos en el experimento piloto, del /cinco/ al /nueve/
El corpus principal, de 1100 dígitos pronunciados por 11 locutores (numerados del 1 al 11), se utilizó en 6 experimentos sencillos y dos experimentos en los que se utilizó la técnica "Leaving-k-out" (cross-validation) [Raudys,91] para suplir la relativa pequeñez del corpus.
Los experimentos sencillos se resumen en la tabla 8.5. Se encuentra un experimento multilocutor (H2) y varios independientes del locutor. H1,H3,H4 pretender estudiar cómo afecta la mayor o menor cantidad de muestras de aprendizaje con respecto a las utilizadas posteriormente para el test de reconocimiento. H5, realizado posteriormente utiliza el reparto más adecuado con todas las muestras disponibles. H6 sustituye el locutor 10 de H5, que demostró estar adquirido en condiciones inadecuadas (saturación, palabras cortadas, etc...).
| Exp.
|
Aprendizaje
|
Test
|
Descripción
|
| Id.
deLocutores, Sexo, NºMuestras
|
Id.
de Locutores, Sexo NºMuestras
|
||
| H1
|
1,3,4,7,8 2F,3M
5*10*10=500
|
2,5,9,10 3F,2M
5*5(primeras)*10=250
|
Independiente
del locutor, mitad y mitad de las muestras
|
| H2
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*5(primeras)*10=500
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*5(siguientes)*10=500
|
Multilocutor
|
| H3
|
1,2,5,6,7,8,9,10 4F,4M
8*6(primeras)*10=480
|
3,4 1M,1F
2*10*10=200
|
Independiente
del locutor, más locutores en aprendizaje
|
| H4
|
3,5,6,9 2F,2M
4*10*10=400
|
1,2,4,7,8,10 3F,3M
6*3(primeras)*10=180
|
Independiente
del locutor, pocos locutores en aprendizaje
|
| H5
|
1,2,4,7,8,10 3F,3M
6*10*10=600
|
3,5,6,9 2F,2M
4*10*10=400
|
Independiente
del locutor, todas las muestras, locutor 10 mal adquirido.
|
| H6
|
1,2,4,7,8,11 3F,3M
6*10*10=600
|
3,5,6,9 2F,2M
4*10*10=400
|
Independiente
del locutor, todas las muestras.
|
| Algoritmo
de Reconocimiento
|
H1
|
H2
|
H3
|
H4
|
H5
|
H6
|
| No
estocástico
|
||||||
| Modelo
de error completo
|
-
|
-
|
-
|
-
|
98,5
|
99
|
| Sólo
substituciones
|
-
|
-
|
-
|
-
|
99,5
|
99,5
|
| Estocástico
|
||||||
| Modelo
de error completo
|
99,2
|
-
|
-
|
-
|
100
|
100
|
| Ignorando
frecuencia de errores
|
97,6
|
-
|
-
|
-
|
-
|
-
|
| Sólo
substituciones
|
98
|
100
|
100
|
98,8
|
99,7
|
99,8
|
| Sólo
substituciones, ignorando frecuencia de reglas
|
96,8 |
100 |
99,5 |
96,6 |
99,5 |
99,8 |
| Sólo
substituciones, ignorando frecuencia de errores
|
97,6 |
99,8 |
100 |
98.8 |
99 |
99 |
| Número
medio de estados
|
153
|
172
|
159
|
146
|
171
|
158
|
En en caso no estocástico, es interesante comprobar que prohibir errores de inserción y borrado mejora el reconocimiento, llevándolo del 99% al 99,5%. Posiblemente debido a que (como indica el caso de utilizar sólo substituciones, pero ignorando las frecuencias de error en el modelo estocástico) (ver capítulo 9) las reglas de error incorporadas al autómata toman demasiada importancia si se les superpone las del modelo de error, a menos que se hallen presentes las probabilidades de las reglas para suavizar el efecto.
Como es posible comprobar con el experimento H4 (40 muestras por autómata frente a 50..60 en los demás experimentos), una disminución de muestras en aprendizaje conlleva un empeoramiento notable de la efectividad de los modelos en aprendizaje.
Por otro lado, el número de muestras utilizadas en reconocimiento (500 en el mejor de los casos) tampoco es realmente suficiente para estimar la capacidad de reconocimiento de ECGI. En [Duda,73] se estudia formalmente esta cuestión y se presenta una tabla en la que aparece el intervalo de confianza de una estimación del error medio real (y desconocido) p de un clasificador, en función del error estimado y del número de muestras utilizadas para la estimación n. Aún en el caso de que sea nulo (no hayan errores de reconocimiento), si se han utilizado 250 muestras, p se halla (con un 0.95 de probabilidad) entre el 0 y 0.6%. Con 1000 muestras todavía podría estar entre el 0 y 0.2%.
Para paliar el inconveniente de disponer tan sólo de un conjunto reducido de muestras, a la hora de estimar las capacidades de un reconocedor, se suele recurrir, en reconocimiento de formas, a la técnica de "leaving-k-out" [Raudys,91]. Esta técnica consiste en repetir varias veces los experimentos de reconocimiento intercambiando cada vez parte del conjunto de aprendizaje con parte del de test.
En nuestro caso se han repetido 5 veces un experimento de reconocimiento, intercambiando cada vez las muestras pertenecientes a 2 locutores (uno masculino y otro femenino). De esta manera, cada experimento sigue siendo independiente del locutor y se disponen cada vez de 800 muestras de aprendizaje (80 por autómata) y 200 de test, dando lugar a un conjunto de test efectivo de 1000 muestras. A lo largo de este trabajo hemos llamado HLKO11 este conjunto de experimentos (tabla 8.7).
| Exp.
|
Aprendizaje
|
Test
|
| Locutores
Sexo NºMuestras
|
Locutores
Sexo NºMuestras
| |
| H11
|
2,4,5,6,7,8,9,11
4F,4M 8*10*10=800
|
1,3
1F,1M 2*10*10=200
|
| H22
|
1,3,4,5,6,8,9,11
4F,4M 8*10*10=800
|
2,7
1F,1M 2*10*10=200
|
| H33
|
1,2,3,5,6,7,9,11
4F,4M 8*10*10=800
|
4,8
1F,1M 2*10*10=200
|
| H44
|
1,2,3,4,6,7,8,11
4F,4M 8*10*10=800
|
5,9
1F,1M 2*10*10=200
|
| H55
|
1,2,3,4,5,7,8,9
4F,4M 8*10*10=800
|
6,11
1F,1M 2*10*10=200
|
| Algoritmo
de Reconocimiento
|
H11
|
H22
|
H33
|
H44
|
H55
|
Total
|
| No
estocástico
|
||||||
| Modelo
de error completo
|
99,5
|
99
|
99,5
|
100
|
99,5
|
99,5
|
| Sólo
substituciones
|
99,5
|
99,5
|
99
|
100
|
99,5
|
99,5
|
| Estocástico
|
||||||
| Completo
|
100
|
99,5
|
100
|
100
|
99,5
|
99,8
|
| Sólo
substituciones
|
100
|
99,5
|
100
|
100
|
99,5
|
99,8
|
| Número
medio de estados
|
181
|
200
|
199
|
186
|
198
|
192
|
Es muy notable el que, al aumentar las muestras de aprendizaje, los resultados del modelo de error completo y del obtenido prohibiendo los errores de borrado e inserción coinciden. Ello confirma que los modelos inferidos han ido incorporando los errores más frecuentes, e implica evidentemente un aumento de la complejidad espacial de los autómatas. Este aumento no es sin embargo excesivo, pues, en el peor de los casos, ha sido sólo de un 26% (comparando H4, de sólo 400 de muestras de aprendizaje y H22, de 800), y en el mejor 7.5% (H2, de 500 muestras, con H44).
Una idea de la estructura de los autómatas inferidos se puede extraer de la tabla 8.9 (todas las cantidades son medias para los 50 autómatas).
aprendizaje min. med. max.
6,25.1014 192,8 1,97 387 28,3 15,4 19,9 55,1
El número de estados de los autómatas varía de 126 a 340 (ver apéndice B para detalles).
Los mismos experimentos, pero utilizando el locutor 10, demuestran que éste efectivamente es muy distinto a los demás (mala adquisición, comprobada examinando la señal en el dominio del tiempo), pues los resultados empeoran sensiblemente al estar este locutor en el conjunto de test (H55) (tabla 8.10).
| Algoritmo
de Reconocimiento
|
H11
|
H22
|
H33
|
H44
|
H55
|
Total
|
| Estocástico
|
||||||
| Modelo
de error Completo
|
100
|
99
|
100
|
100
|
97,5
|
99,3
|
| Sólo
substituciones
|
100
|
99
|
100
|
100
|
97,5
|
99,3
|
| Número
medio de estados
|
210
|
210
|
209
|
196
|
198
|
205
|
El corpus de 3000 letras habladas se utilizó en 4 experimentos sencillos y uno utilizando la técnica de "Leaving-k-out", con la misma filosofía que la aplicada en el corpus principal de dígitos hablados.
De los 4 experimentos sencillos, los 3 primeros fueron multilocutor y el cuarto independiente del locutor. En los dos primeros se utilizó un subconjunto del corpus, una vez escogiendo un rango cualquiera de letras ('H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q') y la otra, el especialmente difícil conjunto de las EE-Letras. En los dos últimos se experimentó con las 30 clases posibles, una vez multilocutor y la otra independiente del locutor (ver tabla 8.11).
| Exp.
|
Aprendizaje
|
Test
|
Descripción
|
| Id.
deLocutores, Sexo, NºMuestras
|
Id.
de Locutores, Sexo, NºMuestras
|
||
| L1
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*8(primeras)*9=720
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*2(últimas)*9=180
|
Multilocutor,
vocabulario: "H,I,J,K,L,M,N,O,P,Q"
(9 letras)
|
| L2
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*8(primeras)*9=720
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*2(últimas)*9=180
|
Multilocutor,
vocabulario: "F,L,LL,M,N,Ñ,R,RR,S"
(9 letras)
|
| L3
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*8(primeras)*30=2400
|
1,2,3,4,5,6,7,8,9,10 5F,5M
10*2(últimas)*30=600
|
Multilocutor,
vocabulario: Todas las letras.
(30 letras)
|
| L4
|
1,2,3,4,5,8 3F,3M
6*10*30=1800
|
6,7,9,10 2F,2M
4*10*30=1200
|
Independiente
del locutor, vocabulario: Todas las letras (30 letras).
|
| L1
|
L2
|
L3
|
L4
|
| 99
|
86,7
|
86
|
76,5
|
Para obtener una estimación del comportamiento de ECGI en un caso aún más difícil, se repitió el experimento L2 (EE-letras), pero en el caso independiente del locutor. Para aumentar la fiabilidad de los resultados se recurrió a la técnica de "leaving-k-out". Se realizó pues 5 veces el experimento, utilizando dos locutores en la fase de test (uno masculino y otro femenino) e intercambiando en cada experimento estos dos locutores con otros dos del conjunto de aprendizaje. Con ello se dispone en cada experimento de 720 muestras de aprendizaje (72 por autómata) y 180 de test (llamamos LLKO a este experimento), dando lugar a un conjunto de test efectivo de 900 muestras (tabla 8.13).
| Exp.
|
Aprendizaje
|
Test
|
| Locutores
Sexo NºMuestras
|
Locutores
Sexo NºMuestras
| |
| L11
|
3,4,5,6,7,8,9,10
4F,4M 8*10*9=720
|
1,2
1F,1M 2*10*9=180
|
| L22
|
1,2,5,6,7,8,9,10
4F,4M 8*10*9=720
|
3,4
1F,1M 2*10*9=180
|
| L33
|
1,2,3,4,6,7,9,10
4F,4M 8*10*9=720
|
5,8
1F,1M 2*10*9=180
|
| L44
|
1,2,3,4,5,7,8,10
4F,4M 8*10*9=720
|
6,9
1F,1M 2*10*9=180
|
| L55
|
1,2,3,4,5,6,8,9
4F,4M 8*10*9=720
|
7,10
1F,1M 2*10*9=180
|
| Algoritmo
de Reconocimiento
|
L11
|
L22
|
L33
|
L44
|
L55
|
Total
|
| No
estocástico
|
||||||
| Modelo
de error completo
|
76,1
|
73,8
|
71,1
|
68,3
|
60
|
69,9
|
| Estocástico
|
||||||
| Completo
|
77,7
|
76,1
|
76,6
|
72,2
|
66,6
|
73,8
|
| Ignorando
frecuencia de reglas
|
72,2
|
73,9
|
72,2
|
67,8
|
62,2
|
69,8
|
| ignorando
frecuencia de errores
|
76,7
|
77,2
|
70
|
70
|
62,8
|
71,3
|
| Número
medio de estados
|
831
|
784
|
797
|
763
|
749
|
785
|
En la matriz de confusión media de los 5 experimentos se puede comprobar que la letra que da más problemas para su reconocimiento es la N (que se confunde con la M y Ñ), seguida de la L (que se confunde con la LL y R), lo cual es completamente consistente con nuestra apreciación perceptiva de la dificultad de la tarea (tabla 8.15).
F 82 1 0 0 0 0 0 2 15 82%
L 0 55 16 5 1 2 14 7 0 55%
LL 0 15 78 0 0 5 1 0 1 78%
M 1 3 0 70 6 13 1 6 0 70%
N 1 5 0 24 43 21 6 0 0 43%
Ñ 2 2 5 3 1 87 0 0 0 87%
R 0 23 1 4 2 1 69 0 0 69%
RR 3 6 0 2 0 0 0 89 0 89%
S 11 0 0 0 0 0 0 0 89 89%
ToTal 73,5
Las cantidades que resumen la estructura media de los 45 autómatas se dan en la tabla 8.16.
aprendizaje min. med. max.
1,2.1026 785 1,62 1271 56,8 26,8 51,8 130,3
La mayor cantidad media de reglas (3 veces más) de estos autómatas, si se les compara con los de los dígitos hablados, es debida no sólo a que las cadenas son el doble de largas en promedio, sino también a la mucha mayor variabilidad inducida por la existencia del doble número de símbolos.
Aunque ECGI surgió durante la búsqueda de una solución para un determinado problema de reconocimiento del habla, fué evidente desde un principio que representaba una metodología aplicable a muchos otros campos del reconocimiento de formas.
Los siguientes experimentos se llevaron a cabo para demostrar esta independencia de ECGI de un campo de aplicación concreto, y pusieron en evidencia una vez más su eficacia como método de reconocimiento de formas.
Hay que hacer notar que los resultados obtenidos, y que se muestran a continuación, se han conseguido sin ningún tipo de adaptación de ECGI al problema concreto del reconocimiento de imágenes.
La adquisición, parametrización y conversión en una cadena de las imágenes se realiza siguiendo el procedimiento esquematizado en el capítulo 1. Más concretamente, todos los experimentos se han realizado a partir de muestras de dígitos (arábicos) manuscritos o impresos, adquiridas mediante una cámara que proporciona una imagen de 512*512 pixels, con una resolución de 3 pixels/mm.
Una vez digitalizada la imagen a 8 bits/pixel, se aplica un umbral para reducirla a 1 bit/pixel, suprimiendo así los grises. Seguidamente un barrido de izquierda a derecha y de arriba abajo, detecta la parte superior izquierda de cada uno de los dígitos individuales. Este es el primer punto del contorno de dicho dígito. A continuación, se aplica un algoritmo de seguimiento de contornos [Freeman,74], que proporciona la dirección en la que se encuentra el siguiente punto del contorno, de entre las 8 posibles. La secuencia de direcciones, codificadas del 0 al 7 (figura 8.7), proporciona la cadena de símbolos correspondiente a la imagen.
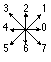
No se ha aplicado ningún procedimiento para asegurar la invarianza de la representación con respecto al giro y a la escala. La invarianza a la posición es intrínseca a la representación. Por lo tanto, se supondrá que ECGI es perfectamete capaz de tener en cuenta, gracias a su capacidad de generalización y corrección de errores, pequeñas variaciaciones de giro, inclinación y tamaño de los caracteres.
La resolución original de la imagen de 3 pixels/mm., proporciona cadenas largas, con gran cantidad de información probablemente redundante. Conocida la capacidad de ECGI de obtener resultados con muy poca información, se decidió disminuir esta resolución progresivamente, mediante aplicación de 4 rejillas de separación respectivamente de 4, 6, 8 y 10 pixels sobre la imagen original (figura 8.8). Un objetivo añadido de los experimentos consiste pues en determinar la rejilla (resolución, o lo que es igual: longitud de las cadenas) máxima que nos proporcione resultados óptimos.

El corpus de los dígitos manuscritos está formado por 20 repeticiones de cada dígito, escritas por 12 personas diferentes (2400 dígitos en total).
Cada escritor, utilizando un rotulador grueso, escribió los dígitos en hojas de papel blanco, en las que ya figuraban unas líneas guía inferiores, muy ténues. La única condición impuesta a los escritores fue que los dígitos se escribieran separados unos de otros. No se mencionó ninguna restricción de tamaño ni estilo (aunque las líneas guía y el grosor del rotulador impidieran fantasías excesivas), observándose finalmente una variación 1:1/2 en tamaño y variaciones de inclinación del orden de -10 a +20 grados.
Al igual que en el experimento HLKO de los dígitos hablados, se recurrió a la técnica del "leaving-k-out". Se realizaron 12 experimentos, en cada uno de ellos se utilizaron las muestras de 10 de los escritores (2000 cadenas) para el aprendizaje y las de los dos restantes para test (400 cadenas). Por lo tanto, en todos los casos las cadenas de test pertenecían a escritores diferentes que los de las cadenas de aprendizaje. Cada experimento se diferencia del anterior por permutación circular del papel de cada uno de los escritores (tabla 8.17). De esta manera el total de operaciones de reconocimiento se eleva a 4800, habiéndose generado 120 autómatas a partir de 200 cadenas cada uno.
| Exp.
|
Aprendizaje
|
Test
|
| Escritores
NºMuestras
|
Escritores
NºMuestras
| |
| M1
|
3,4,5,6,7,8,9,0,A,B
10*20*10=2000
|
1,2
2*20*10=400
|
| M2
|
1,4,5,6,7,8,9,0,A,B
10*20*10=2000
|
2,3
2*20*10=400
|
| ...
|
...
|
...
|
| M12
|
1,2,3,4,5,6,7,8,9,0
10*20*10=2000
|
A,B
2*20*10=400
|
Los autómatas se infirieron utilizando el criterio maxA (definido en 6.6). Cada experimento de "leaving-k-out" se repitió variando el algoritmo de reconocimiento; obteniéndose los resultados mostrados en la tabla 8.18.
| Algoritmo
de Reconocimiento
|
Rej4
|
Rej6
|
Rej8
|
Rej10
|
| No
estocástico
|
||||
| Modelo
de error Completo
|
92,3
|
92
|
91
|
89
|
| Sólo
substituciones
|
92,5
|
92
|
91
|
89,4
|
| Estocástico
|
||||
| Modelo
de error Completo
|
98,4
|
98,3
|
96,9
|
96,0
|
| Sólo
substituciones
|
98
|
98,1
|
96,9
|
96,3
|
Por otro lado, y como se esperaba, al aumentar la resolución de la rejilla la tasa de error disminuye. Sin embargo, la mejora obtenida al pasar de la rejilla de resolución 8 a la 6 es muy superior a la obtenida al pasar de la 6 a la 4, casi insignificante, por lo que no resulta útil emplear esta última.
En la tabla 8.19, se muestra la matriz de confusión media de los 12 reconocimientos efectuados para la rejilla 6 en el caso estocástico de sólo substitución en reconocimiento. La matriz correspondiente al modelo de error completo es muy similar (véase apéndice B para poder comparar las 4 rejillas).
0 474 0 0 0 0 0 3 0 3 0 98.7%
1 0 467 8 0 0 0 0 0 0 5 97.3%
2 0 0 480 0 0 0 0 0 0 0 100.0%
3 0 0 0 480 0 0 0 0 0 0 100.0%
4 0 1 0 0 465 0 0 4 0 10 96.9%
5 0 0 0 0 0 480 0 0 0 0 100.0%
6 0 0 0 0 0 0 480 0 0 0 100.0%
7 0 2 0 0 0 0 0 476 0 2 99.2%
8 0 0 12 6 1 0 1 0 453 7 94.4%
9 0 2 0 12 0 6 0 0 4 456 95.0%
Seguidamente se tabulan las tasas de error, para cada uno de los autómatas y cada uno de los 12 reconocimientos (R1 a R12) efectuados con las 4 rejillas, también cuando sólo se permiten substituciones en reconocimiento.
R1 99,7 99,7 98,7 98,7 99,2
R2 98,7 99 98,5 98,2 98,6
R3 99,2 98,7 98,2 97 98,3
R4 100 99,2 99,5 96,5 98,8
R5 96 98 95,7 94,7 96,2
R6 93,5 95 92,7 90,7 93,7
R7 97,2 98 96,2 94,7 96,5
R8 98,2 97,7 97,5 98,7 98,3
R9 97 96,5 96,5 96,5 96,6
R10 98,7 98,2 97 97 97,7
R11 99,7 99 96,2 97,5 98,1
R12 98,7 98,5 96 95,2 98,1
Media 98 98,1 96,9 96,3
Una idea de la estructura y dimensiones espaciales de los autómatas se puede extraer de la tabla 8.21.
| Rej4
|
Rej6
|
Rej8
|
Rej10
| |
| Tamaño
del Lenguaje
|
5,6.1060
|
1,8.1040
|
1,0.1031
|
8,5.1023
|
| Número
medio de estados
|
309
|
223
|
175
|
144
|
| Factor
de Ramificación
|
3,78
|
3,71
|
3,70
|
3,60
|
| Nº
de Reglas
|
1170
|
826
|
649
|
519
|
| Longitud
Cadenas Corpus
|
73,1
|
48,1
|
35,7
|
28,3
|
| Longitud
de cadenas Aceptadas
|
||||
| mínima
|
22
|
16
|
13
|
11
|
| máxima
|
182
|
120
|
91
|
71
|
| media
|
80
|
52
|
39
|
30
|
El corpus de los dígitos impresos está formado por caracteres impresos con 8 diferentes tipos de letra. Cada tipo se ha impreso con 4 tamaños diferentes en el rango 1:1/2. Para cada tamaño de cada tipo se imprimió cada dígito 10 veces, 5 en negrita y 5 en grosor normal. Para cada tipo de letra hay por lo tanto 4*(5+5)*10=400 muestras, estando el corpus completo constituído por 3200 imágenes. En la figura 8.10 se muestra un ejemplo representativo de las mismas.
C. Font Normal Negrita
1 Avant Garde 0123456789 012456789
2 Bookman 0123456789 0123456789
3 Courier 0123456789 0123456789
4 Helvética 0123456789 0123456789
5 New Century 0123456789 0123456789
6 Palatino 0123456789 0123456789
7 Times 0123456789 0123456789
8 Zapf Chancery 0123456789 0123456789
Tamaño
0000 1111 2222 3333 4444 5555 6666 7777 8888 9999
Utlizando la técnica del "leaving-k-out" se realizaron 8 experimentos, en cada uno de ellos se utilizaron las muestras correspondientes a 7 tipos de letra para el aprendizaje (2800 cadenas), y la restante para el reconocimiento (400 cadenas). Por lo tanto, las cadenas de test pertenecían, en todos los casos, a un tipo de letra distinto que el de las utilizadas en aprendizaje. Cada experimento se diferencia del anterior por permutación circular del papel de cada uno de los tipos. De esta manera el total de operaciones de reconocimiento se eleva a 3200, habiéndose generado 80 autómatas a partir de 280 cadenas cada uno (tabla 8.22).
| Exp.
|
Aprendizaje
|
Test
|
| Tipos
NºMuestras
|
Tipos
NºMuestras
| |
| I
1
|
2,3,4,5,6,7,8
7*40*10=2800
|
1
1*40*10=400
|
| I
2
|
1,3,4,5,6,7,8
7*40*10=2800
|
2
1*40*10=400
|
| ...
|
...
|
...
|
| I
8
|
1,2,3,4,5,6,7
7*40*10=2800
|
8
1*40*10=400
|
Los autómatas se infirieron utilizando el criterio maxA (definido en 6.6). Cada experimento de "leaving-k-out" se repitió con el modelo de error completo y prohibiendo inserciones y borrados; obteniéndose los resultados mostrados en la tabla 8.23.
| Algoritmo
de Reconocimiento
|
Rej4
|
Rej6
|
Rej8
|
Rej10
|
| Estocástico
|
||||
| Completo
|
99,4
|
99,8
|
99,6
|
98,2
|
| Sólo
substituciones
|
99,9
|
99,4
|
98,9
|
97,7
|
Con el modelo de error completo resulta ser ventajoso limitarse a la rejilla de resolución 6. Si sólo se autorizan sustituciones la variación de la rejilla 8 a la 4 es casi lineal, pudiéndose entonces considerar la rejilla 6, al igual que para los dígitos manuscritos, como un buen compromiso en caso de necesidad imperiosa de reducir la complejidad espacial y temporal.
Los resultados, como era de esperar, son mejores que los obtenidos en los experimentos equivalentes de dígitos manuscritos, situándose aproximadamente en un 1,5% en el caso de sólo substitución. Con el modelo de error completo, en las bajas resoluciones de la rejilla (8 y 10) se llega a más de un 2% de diferencia.
A continuación (tabla 8.24) se muestra la matriz de confusión media de los 8 reconocimientos efectuados para la rejilla 6 en el caso de sólo substitución en reconocimiento. La matriz correspondiente al modelo de error completo es muy similar (véase apéndice B para poder comparar las 4 rejillas).
0 319 0 0 0 0 0 0 0 1 0 99.7%
1 0 309 0 0 0 0 0 11 0 0 96.6%
2 0 0 320 0 0 0 0 0 0 0 100.0%
3 0 0 0 320 0 0 0 0 0 0 100.0%
4 0 1 0 0 320 0 0 0 0 0 100.0%
5 0 0 0 0 0 320 0 0 0 0 100.0%
6 0 0 0 0 0 0 316 0 4 0 98.8%
7 0 0 0 0 0 0 0 320 0 0 100.0%
8 1 0 0 0 0 0 0 0 319 0 99.7%
9 0 0 0 0 0 0 0 0 1 319 99.7%
Seguidamente se tabulan las tasas de error, para cada uno de los autómatas y cada uno de los 8 (R1 a R8) reconocimientos efectuados con las 4 rejillas, también cuando sólo se permiten substituciones en reconocimiento (tabla 8.25).
R1 99,75 99,75 96 94,25 97,43
R2 100 99,75 100 98 99,43
R3 100 100 99,25 99 99,5
R4 100 100 99 99,25 99,56
R5 100 100 100 96,75 99,18
R6 100 100 100 99,25 99,18
R7 100 100 100 99,25 99,8
R8 100 100 97 95,5 98,12
Media 99,97 99,44 98,91 97,75
Donde se observa claramente que el tipo que más difícil es de reconocer es el que sirve de test en el primero de los 8 reconocimientos: el tipo AvantGarde (0123456789). Este tipo es, con el Helvetica (0123456789) el único que no tiene serif, y tiene los 6 y 9 mucho más abiertos que todos los otros tipos. El siguiente tipo en dificultad es el ZapfChancery (0123456789), del cual se esperaba que fuera el más difícil por su estilo mucho más curvilíneo.
Una idea de la estructura y dimensiones espaciales de los autómatas se puede tener examinando la tabla 8.26.
| Rej4
|
Rej6
|
Rej8
|
Rej10
| |
| Tamaño
del Lenguaje
|
3,3.1045
|
1,2.1036
|
5,4.1026
|
6,2.1020
|
| Número
medio de estados
|
255
|
174
|
134
|
114
|
| Factor
de Ramificación
|
3,57
|
3,46
|
3,34
|
3,22
|
| Nº
de Reglas
|
911
|
602
|
449
|
369
|
| Longitud
Cadenas Corpus
|
72,8
|
47,9
|
35,5
|
28,1
|
| Longitud
de cadenas Aceptadas
|
||||
| mínima
|
22
|
17
|
14
|
12
|
| máxima
|
154
|
101
|
75
|
60
|
| media
|
66
|
42
|
30
|
24
|
Con exactamente la misma filosofía descrita en el apartado anterior, se repitieron todos los experimentos en los que sólo se autorizaba substitución y en los que se utilizaba el modelo de error completo, pero quitando del conjunto de muestras, una vez el ZapfChancery, y otra el Helvética. Los resultados se muestran en la tabla 8.27.
| Algoritmo
de Reconocimiento
|
Rej4
|
Rej6
|
Rej8
|
Rej10
|
| Todos
Los Tipos
|
||||
| Completo
|
99,4
|
99,78
|
99,59
|
98,22
|
| Sólo
substituciones
|
99,97
|
99,44
|
98,91
|
97,75
|
| Sin
ZapfChancery
|
||||
| Completo
|
99,93
|
99,75
|
99,43
|
98,50
|
| Sólo
substituciones
|
100
|
99,29
|
99,32
|
97,82
|
| Sin
Helvética
|
||||
| Completo
|
99,36
|
99,75
|
98,82
|
98,50
|
| Sólo
substituciones
|
99,18
|
98,75
|
98,14
|
97,32
|
Por otra parte, resulta interesante comprobar cómo ECGI modeliza efectivamente las características más importantes de las formas consideradas. Examinando con detalle los resultados del experimento sin tipo Helvética, se comprueba que en todos los casos (con rejilla 4 y 6) se obtuvo un 100% de aciertos excepto en el primero de los 8 reconocimientos, el R1, en el que se obtuvieron las tasas mostradas en la tabla 8.28.
Completo 95,5 94,25
Sólo substituciones 98,25 91,25
Lo que evidencia que la única dificultad se presenta cuando el tipo AvantGarde esta en el conjunto de test. Del examen de las matrices de confusión (en apéndice B) se desprende que en un 71% de los casos el error es debido a confundir un 1 con un 7. Es decir, en vez de asignar (1) a la clase cuyo modelo se ha aprendido mediante (111111), se le asigna a la clase correspondiente a (777777), lo cual evidentemente es debido a dos obvias característica diferenciadora del (1) de AvantGarde: no tiene la "base" debida al serif, y la parte superior del uno es horizontal en vez de dirigirse hacia abajo. Ello es tanto más relevante, en cuanto el único error que se produce en el experimento con todos los tipos (correspondiente al valor 99,97% de aciertos: 1 error de 3200 muestras, sólo substitución con rejilla 4) es debido a la misma confusión de (1) de AvantGarde con un 7 (véase matrices de confusión en el apéndice B), y ello aunque ECGI haya aprendido, gracias a Helvética que existen unos sin serif: (1) (figura 8.12).
Como ya se expuso, al hablar del método de parametrización y conversión de imágenes planas a cadenas, la representación utilizada en los experimentos no es en absoluto invariante a la rotación ni al cambio de escala. Se ha comprobado, a través de los resultados obtenidos, que ECGI es capaz de adaptarse a pequeñas variaciones de escala y ángulo de presentación de los objetos, recurriendo a sus capacidades de generalización. No ocurre lo mismo si las variaciones de tamaño y de inclinación son muy amplias, pues ello llevaría a un crecimiento desmesurado de los modelos inferidos por ECGI, al tener éstos que dar cuenta de todas las posibilidades de presentación. Afortunadamente, una invarianza a la escala es fácilmente obtenible mediante una adaptación automática de la resolución de la rejilla.
Sin embargo, la invarianza a la rotación presenta mayores inconvenientes. Una posibilidad podría ser el utilizar códigos de cadena relativos [Bribiesca,80], en los que cada símbolo representa un ángulo relativo al anterior y no un ángulo absoluto como aquí se ha definido. Todos los contornos de un mismo objeto en distintas rotaciones, codificado de esta manera, proporcionará la misma cadena circular. Desafortunadamente, dependiendo del punto de corte se obtendrán diferentes cadenas lineales.
En casi todos los casos, en aprendizaje sigue siendo posible presentar los objetos patrón en una posición específica, lo cual permite cortar las cadenas circulares en un punto fijo (p.e. la parte superior izquierda) y aplicar continuación ECGI en aprendizaje como es usual. En reconocimiento, sin embargo, será necesario aplicar un proceso de comparación que tenga en cuenta la posible permutación circular de las cadenas.
También es posible el reconocimiento de dígitos trazados, en los que se adquiere directamente una secuencia de direcciones, la cual es mucho más significativa que la proporcionada por los contornos. Si se prescinde del problema de la invarianza a la rotación, ECGI es inmediatamente aplicable a este tipo de adquisición con sólo realizar una adecuada normalización de escala (y quizá algún filtrado).
Por otra parte, no es imprescindible representar las imágenes mediante contornos (pueden utilizarse esqueletos por ejemplo [Davies,81] [Zhang,84]), ni siquiera mediante modelos lineales. Es extremadamente sencillo extender los algoritmos que mediante corrección de errores realizan la comparación de una cadena con una gramática, es decir de una estructura lineal (la cadena) con una arbórea (la gramática), de manera que permitan comparar dos estructuras arbóreas. Así se podría conseguir que encontraran (p.e.) la cadena más similar entre dos gramáticas, o comparar una estructura arbórea (e incluso quizás una red en general) con otra (una estructura arbórea con una gramática de Web o de árbol [Fu,82]). Ello permitiría utilizar ECGI para inferir modelos de estructuras no lineales.
Una posible aproximación, para comprobar hasta qué punto los modelos inferidos por ECGI modelizan las formas que se suponen deben representar, consiste en utilizar los autómatas inferidos en la síntesis de nuevas muestras (objetos), y compararlos "de visu" con objetos reales.
Ello es especialmente factible en el caso de imágenes, las cuales presentan además la ventaja --que no tendría un experimento de síntesis de la palabra-- de proporcionar resultados fácilmente mostrables.
El algoritmo de síntesis consiste simplemente en un recorrido aleatorio de las reglas de la gramática: partiendo del axioma se llega hasta una regla final (A->a), escogiendo en cada paso al azar la siguiente regla a aplicar. La decisión aleatoria tiene en cuenta las probabilidades de las reglas (pero no las de error: no se pretende añadir a las cadenas sintetizadas errores provenientes del modelo de error). Este proceso se ha utilizado para generar las muestras de las figuras siguientes, que presentan cada una 100 muestras. Las muestras (figura 8.13), en un primer caso (parte superior de la la figura) han sido generadas con los autómatas inferidos a partir del corpus de dígitos manuscritos, y en un segundo caso (parte inferior de la figura) a partir del de dígitos impresos.
Del conjunto de resultados presentados a lo largo de todo este capítulo, se puede comprobar la gran eficacia que tiene el método ECGI en el reconocimiento de formas, por poco que el problema se adapte a los heurísticos que el método lleva implícitos.
En reconocimiento del habla, los resultados son similares o superiores a los proporcionados por otros métodos de reconocimiento de palabras aisladas, usualmente considerados como los que más eficaces en la práctica (modelos de Markov (HMM), alineamiento temporal (DTW),...) (ver capítulo 12). En tareas de reconocimiento de dígitos hablados (independientes del locutor, en ambiente no ruidoso) se consigue con ECGI tasas de aciertos superiores al 99% en todos los casos, llegando sin especial dificultad al 99,8% e incluso al 100% en algunos casos. Para diccionarios difíciles, como las letras, y especialmente las EE-letras, los resultados son también similares a los que proporcionan otras técnicas: 76,5% de aciertos para las 26 letras castellanas y 73.8% para las 9 EE-letras. Como punto de comparación, se puede mencionar que en [Casacuberta,91] se obtiene un 75% en este último corpus, mientras que en [Bahl,87] se obtiene (con HMM) un 92% reconociendo el E-set inglés, pero utilizando símbolos no cuantizados vectorialmente. Los resultados de [Bahl,87] bajan a un 79% si se procede a la cuantización, aunque se muestree a 100Hz., en vez de los 66.6Hz. de los experimentos aquí presentados. Por otro lado, ECGI consigue muy buenos resultados (99.5%, dependiente del locutor) incluso con cadenas formadas por símbolos muy poco elaborados y con relativamente pocas muestras de aprendizaje (38 por clase).
En reconocimiento de imágenes (en concreto dígitos manuscritos e impresos), los resultados son similarmente satisfactorios, realmente mejores que otros métodos más clásicos (98% frente a 80-90% obtenidos mediante la utilización de momentos geométricos y distancia de Mahalanobis [Vidal,92] [Vidal,92a], ver capítulo 12) y similares a las mejores que se obtienen actualmente con métodos mucho más adaptados a la tarea específica (98-99% [Kurosawa,86] [ Shridar,86] [Baptista,88]).
Por otra parte, los experimentos han mostrado la real y necesaria aportación que lleva a cabo la información estadística al reconocimiento (la inferencia ha sido en todos los casos no estocástica), ganando ECGI gracias a ella un 5% de promedio en la tasa de reconcimiento. También se ha evidenciado que es posible conseguir los mismos resultados (a veces mejores) incluso suprimiendo parte del modelo de error en reconocimiento (permitiendo tan sólo errores de substitución), lo que reduce fuertemente la complejidad temporal del reconocimiento y permite utilizar otros métodos que llevan a reducir dicha complejidad de hasta un 90% [Torró, 90].
La complejidad espacial (que afecta fuertemente a la temporal) de los modelos inferidos nunca llega a ser excesiva: de 400 reglas en tares sencillas (dígitos hablados) a 1300 en tareas difíciles (EE-letras habladas) y puede ser reducida por los métodos de simplificación que se presentarán en el capítulo 10. En la mayoría de los casos ECGI se comporta "razonablemente", pudiéndose comprobar que los errores de reconocimiento son debidos a muestras notablemente distintas de las utilizadas para el aprendizaje (locutor 11 en dígitos hablados, el uno de AvantGarde en dígitos impresos) o a clases que se prestan a confusión (N se confunde con M y Ñ, L se confunde con LL y R, en letras habladas, 1 se confunde con 7 en dígitos impresos).
Finalmente, se ha comprobado de manera muy visual, mediante experimentos de síntesis de imágenes, que los modelos inferidos por ECGI almacenan realmente suficiente información como para poder generar nuevos objetos de su clase, que evidencian todas las características que los diferencian de las otras clases.
[1]Los experimentos iniciales se llevaron a cabo en un Eclipse C-350 de Data-General, aunque luego se repitieron en el HP9300. Por aquel entonces, el ECGI, integrando inferencia y reconocimiento, y junto con los autómatas inferidos, cabía en 64Kbytes de memoria ([exclamdown]que tiempos aquellos!). Los últimos experimentos se realizaron con la última versión de ECGI, escrita en C y que funciona en un RISC 6000 de IBM (S.O. AIX).
[2]La escala de Mel es una escala, basada en el estudio de la membrana basilar del oído humano, aproximadamente lineal en las bajas frecuencias y logarítmica a medias y altas.
[3] Debería decir: ...que muestran inmundos garabatos indignos del escolar más travieso.