ECGI, tal como se ha presentado en el capítulo anterior, es una herramienta muy eficaz que ya en los experimentos piloto demostró su gran poder de modelización. Proporcionó, desde un primer momento, resultados del orden del 97% aciertos, en experimentos de reconocimiento llevados a cabo sobre dígitos hablados (monolocutor), los cuales se hallaban representados mediante cadenas de símbolos muy poco elaborados (ver capítulo 8: experimentos con corpus piloto).
Sin embargo, aunque mejorable (utilizando símbolos más elaborados, e incluso una representación continua), esta tasa de reconocimiento es aún insuficiente en aplicaciones prácticas; más cuando se aspira a resolver tareas mucho más difíciles, en las que las tasas de aciertos de los mejores métodos descienden drásticamente (multilocutor, grandes diccionarios, diccionarios difíciles, ...). Afortunadamente, existe una vía inmediata para mejorar las capacidades de modelización de las estructuras inferidas por ECGI, la cual se deriva directamente de la constatación de que los autómatas inferidos no han retenido ninguna información relacionada con la importancia relativa de las distintas (sub)estucturas inferidas, es decir, ninguna información relativa a las frecuencias de utilización de las distintas reglas, no terminales y terminales[1]. Esta, es precisamente la información incorporada por los métodos estocásticos, la cual estaría disponible si ECGI infiriera una gramática estocástica.
En los siguientes apartados se expone cómo se han incorporado probabilidades a las reglas de las gramáticas generadas por ECGI, y cómo se han aprovechado estas probabilidades en reconocimiento.
En el caso de que la gramática inferida por ECGI sea no ambigua se pueden obtener, mediante el procedimiento expuesto en el capítulo 2 y con todas las garantías de estocastiscidad, las probabilidades de utilización de las reglas, con sólo llevar la cuenta del número de veces que se utilizan en la generación de las muestras de R+. Sin empargo, en la realidad las gramáticas generadas por ECGI son ambiguas (ver capítulo 9), con lo que en principio se hará necesario disponer de un número mucho mayor de muestras (o una reconsideración repetitiva de R+) y utilizar algún método de reestimación de probabilidades (p.e.: reestimación por Viterbi [Levinson,83] [Rabiner,89]) o también Baum-Welch) que asegure la convergencia y fiabilidad de dicha reestimación (ver también capítulo 2). Una aproximación de este tipo se ha planteado y llevado a la práctica en [Castaño,90] proporcionando resultados satisfactorios, aunque no necesariamente mejores que los aquí obtenidos.
No obstante, estos métodos, relativamente costosos, no son imprescindibles en la práctica y, como se mostrará a continuación, una aproximación no estricta (y por lo tanto subóptima) al problema permite obtener tasas de reconocimiento equivalentes (e incluso, en primera aproximación, mejores) a las de un método estrictamente correcto. En consecuencia, en todo el resto del trabajo actuaremos como si las gramáticas generadas por ECGI no fueran ambiguas, asumiendo que todos los resultados que se obtengan serán probablemente subóptimos.
La utilización de la información estadística para mejorar la estructura inferida por ECGI, es decir, su empleo para realizar la búsqueda de la derivación óptima sobre la que luego se basará la construcción, tropieza con dos dificultades:
* La información frecuencial se renueva a cada muestra.
* No sólo es necesaria la información probabilística
referente a las reglas de la gramática que se ha inferido, sino que
también se debe disponer de la misma información sobre las
demás reglas de la gramática expandida (sobre las reglas
de error), puesto que todas ellas se utilizan para el análisis
sintáctico de las muestras.
La modificación de las frecuencias de uso de las reglas a cada muestra implica que, tras cada de ellas, es necesario renormalizar toda la gramática (es decir, convertir las nuevas frecuencias en probabilidades). Aunque ello, en contra de lo que pueda parecer, no resulta excesivamente gravoso comparado con la complejidad del análisis sintáctico corrector de errores, se ha renunciado (en primera aproximación) a esta posibilidad. Por lo tqnto, en todo el resto de este trabajo, el modelo estocástico se estudiará únicamente con miras a mejorar las capacidades de reconocimiento de ECGI, no utilizándose en ningún caso las probabilidades en el proceso de aprendizaje de la estructura del modelo. Conviene notar que ésta es la sistemática más frecuente en reconocimiento de formas: estimación de probabilidades de un modelo estructural fijo, obtenido sin hacer uso alguno de estas probabilidades.
Una consecuencia de esta decisión, entre otras, es la de imposibilitar la integración aprendizaje-reconocimiento en el caso del aprendizaje continuo, al emplearse algoritmos de optimización distintos en cada etapa.
Por otra parte, hay que notar que el procedimiento de renormalizar a cada muestra no es el único factible si se desea utilizar la información estocástica durante la inferencia de la estructura del modelo generado por ECGI. Existe otra posibilidad intermedia, estudiada en [Castaño,90], que consiste en particionar (o reutilizar) R+ para reestimar las probabilidades. En vez de proceder a una renormalización a cada muestra, se reconoce y construye con las probabilidades estimadas en un paso anterior hasta reunir cierto número de muestras. En ese momento es cuando se procede a la renormalización. Los resultados obtenidos por M.A.Castaño muestran una ligera pérdida (no explicada) en la eficiencia del reconocimiento, pero muestran la factibilidad de la idea.
En cuanto al segundo de los puntos arriba mencionados, que destaca la necesidad de disponer del modelo estocástico también para la gramática expandida, es fácil comprobar que ello es una dificultad inherente al proceso incremental de aprendizaje de ECGI. Renunciando a una aproximación incremental, sería posible prescindir de las probabilidades asociadas a las reglas de error. En efecto, al estar incluído el conjunto de muestras R+ en el lenguaje de la gramática inferida, se pueden estimar las probabilidades de las reglas a partir de R+, puesto que no resulta necesario expandir la gramática para realizar el análisis sintáctico.
De todas maneras, y como se verá en los apartados siguientes, es posible estimar de manera fiable un modelo de error estocástico y muy eficaz.
La estimación de las probabilidades de las reglas de error de la gramática expandida de una gramática G=(N,V,P,S), supone una serie de dificultades que se agudizan más, si cabe en el caso particular de ECGI. En efecto, la misma idea en que se basa el método hace imposible estimar realmente la probabilidad de una regla de error concreta: siempre que alguna es utilizada, el proceso de construcción de ECGI se encarga inmediatamente de anularla generando las reglas mínimas imprescindibles para que dicha regla de error no sea necesaria para reconocer (generar) la nueva muestra (y otras similares).
Por otra parte, aún en el caso de que fuera posible, el enorme número de reglas de error[2]: (2.|V|+1).P, exigiría disponer de un número prohibitivo de muestras de aprendizaje para poder efectuar una estimación aceptable de las probabilidades correspondientes.
Para soslayar ambos problemas, no queda más remedio que renunciar efectivamente a la estimación individual de todas las probabilidades de las reglas de error, y recurrir a una aproximación más "global", agrupando dichas reglas por clases y asignar a cada regla la probabilidad de su clase. Se hace entonces la asunción de que la probabilidad de una regla de error no depende de los no terminales asociados a dicha regla (de la "posición" de la regla). En estas condiciones, en la probabilidad de una regla de error sólo interviene el tipo de ésta (inserción, borrado o sustitución) y el símbolo (no terminal) que tiene asociado, por lo que se pueden agrupar las reglas de error en 2.|V|+|V|2 clases, siendo éste el número de probabilidades que efectivamente hay que estimar.
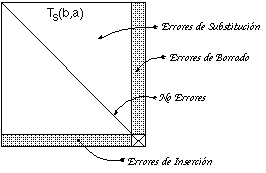
Al no estar estas probabilidades asociadas a una regla en concreto, se puede considerar que una estimación de ellas se puede obtener a partir del conteo de la ocurrencia de las de su clase durante la construcción y/o inferencia de la gramática a partir de R+ (incluso aunque muchas de las reglas que hayan intervenido en el conteo queden anuladas por el proceso de construcción). En consecuencia, ECGI rellena durante la construcción una tabla, que denominaremos Tabla de Sustitución (al considerar inserciones y borrados como sustituciones en las que interviene el símbolo nil [epsilon]), que contiene la frecuencia de sustitución de cada uno de los terminales por otro: fs(b,a) (substitución de 'a' por 'b'), fb(a) (borrado de 'a') y fi(b) (inserción de 'b'). fs(a,a) nos da la frecuencia de las reglas NO erróneas que tienen asociado el símbolo 'a'. f([epsilon],[epsilon]) se define 0.
La tabla de sustitución será por lo tanto una matriz de (|V|+1)2 elementos tales que (En tabla 7.1 se muestra un ejemplo):
K 0 0 32 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 2
N 0 0 0 5 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
O 4 0 2 0 870 0 0 0 1 0 0 0 0 0 3 0 0 0 8
R 0 0 0 0 0 67 0 3 0 0 0 0 0 0 0 0 0 0 3
S 1 0 0 0 0 0 22 1 0 1 0 0 0 0 0 0 0 0 0
T 0 0 0 0 0 0 0 729 2 3 0 3 1 0 0 0 0 0 8
U 0 0 1 2 7 0 0 10 946 0 0 0 8 0 1 0 0 0 3
Z 2 0 0 0 1 1 2 2 0 275 1 0 0 3 1 0 0 0 7
e 2 0 0 1 0 0 0 0 0 0 11 0 0 0 0 0 0 0 2
n 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
o 0 0 1 0 4 0 0 2 2 0 0 0 348 0 2 0 0 0 5
r 3 0 0 0 0 2 0 0 0 1 0 1 0 63 2 0 0 0 3
v 2 0 1 0 4 4 0 2 1 2 2 0 1 1 484 0 0 0 12
# 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
~ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 150 0 0
. 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 150 0
Una vez inferida por ECGI una gramática, es necesario obtener, a partir de la correspondiente tabla de sustitución y de las frecuencias de uso en R+ de las reglas, las probabilidades de éstas y las de las reglas de la gramática expandida; todo ello asegurando la estocasticidad, tanto de la gramática sin expandir como de la expandida.
Utilizando las definiciones dadas en el capítulo 2, si el no terminal A toma parte de las m reglas A->xkBk,k=1...m; de la gramática característica y nk es el número de veces que se utiliza una de ellas rk en R+ basta calcular:
Sin embargo, esta estimación no es válida para el caso del ECGI. Un primer signo de ello se tiene si se observa que, debido a que en la tabla de sustitución las frecuencias de inserción fi(b) no dependen del símbolo anterior (el de la regla), la expresión de Pi(b|xk) depende de xk sólo a través de la normalización. Ello obviamente es consecuencia directa del modelo de error utilizado, y se refleja en el algoritmo ViterbiCorrector, el cual, al construir las reglas de error en el trellis, únicamente añade una regla de inserción por cada símbolo y por cada no terminal a la derecha (y no por cada regla, como obligaría un modelo de error más complejo y que permitiría una dependencia real de xk). Es decir, en el trellis se tendrán las siguientes reglas de error para las m reglas A->xkBk, k=1...m:
A->bBk Ab[propersubset]V; b!=xk ; k=1...m (sustitución)
A->Bk k=1...m (borrado)
A->bA Ab[propersubset]V (inserción)
Esta peculiaridad del modelo de error utilizado por ECGI[3], impide que se pueda utilizar el hecho de que las probabilidades de deformación sean consistentes como garantía de la estocasticidad de la gramática expandida (ver capítulo 2), lo que hace necesario adaptar la condición a este caso particular:
Recuérdese que si G es estocástica y el no terminal A toma parte en las m reglas rk=A->xkBk de probabilidad p(rk), k=1,...,m; se cumple:
ECGI separa totalmente las probabilidades de las reglas de inserción de las de las demás reglas de error. Para ello, se define la probabilidad de inserción de un símbolo 'b', como:
Las otras probabilidades de error se definen siguiendo la filosofía usual, pero aplicando un factor corrector (1-Pi) para asegurar la estocasticidad:
ps(b|xk) = (1-Pi).; pb([epsilon]|xk) = (1-Pi).;
Nx= + fb(xk)
Pi =
Pi representa la probabilidad de inserción de cualquier símbolo en cualquier posición de la gramática, es decir la probabilidad de que se utilize una regla de inserción. (1-Pi) obviamente es la probabilidad de que se emplee cualquier otro tipo de regla. Nótese que Pi también se puede obtener directamente como la la relación entre el número total de inserciones Ni y el número total de errores Ne en R+:
+ =
+ Pi = 1.(1-Pi) + Pi = 1
En resumen, y utilizando las definiciones anteriores, las reglas de error utilizadas por ECGI para el análisis sintáctico corrector de errores estocástico, con sus probabilidades, se derivan de la gramática característica a partir de cada grupo de m reglas A->xkBk k=1...m con el mismo no terminal A a la izquierda, de la siguiente manera:
p(A->bBk) = p(rk).ps(b|xk); Ab[propersubset]V; k=1...m (substitución y no error)
p(A->Bk) = p(rk).pb(xk) k=1...m (borrado)
p(A->bA) = pi(b) Ab[propersubset]V (inserción)
Realizando una pequeña conversión, es posible escribir de otra manera la probabilidad pi(b) de inserción del símbolo 'b':
pi(b) = = . = . = Pi. = Pi.pri(b)
con lo que podemos ponerla en función de la probabilidad de inserción de cualquier símbolo y de la probabilidad relativa de inserción del símbolo 'b' (relación entre la frecuencia de inserción de 'b' y el número total de inserciones):
Tps(b,a) =
Nx= + fb(x); Ni =

Debido al número limitado de cifras significativas de las que dispone un calculador real, y a que en el mismo la rapidez de la adición es usualmente muy superior a la del producto, normalmente se realiza todo el cálculo utilizando los logaritmos de las probabilidades (esto, en su caso, también permitiría trabajar únicamente con enteros):
El mismo proceso se aplica a las probabilidades de las reglas P(r). La contabilización de las frecuencias nk de las reglas rk=(A->xkBk) se realiza también al recorrer la derivación óptima, simultáneamente con la contabilización de las frecuencias de utilización de los no terminales (estados) f(A). Como todas las cadenas que hacen uso de un estado hacen uso de alguna de las transiciones que salen de ese estado, las probabilidades de las reglas se pueden calcular directamente como:
D(Aj,t)=min
Lni = -log(1-Pi); Li = -log(Pi); L(r)= -log(p(r));
donde D(A,t) representa el coste acumulado en el vértice correspondiente al estado A y al terminal t de la cadena en el trellis del análisis sintáctico. Se ha minimizado al tratarse de los logaritmos negados de las probabilidades a maximizar.
Nótese que se ha utilizado la representación hacia atrás (se miran los m predecesores de Aj en lugar de los sucesores). Todo el razonamiento es absolutamente análogo para este caso, y como ya se ha mencionado, es la representación que utiliza la presente implementación de ECGI.
En el capítulo 9 se presenta una tabla resumen de experimentos, que permite comprobar como la aportación de la información estadística mejora sensiblemente las prestaciones de ECGI en reconocimiento de formas. En el mismo capítulo se efectuán también una serie de simplificaciones sobre el modelo aquí presentado, con el fin de comprobar empíricamente cuál es la importancia relativa de la información estadística que aportan las frecuencias de las reglas de la gramática sin expandir y las frecuencias de los distintos errores del modelo de error.
Al igual que en el caso no estocástico en el caso estocástico se ha estudiado la posibilidad de utilizar sólo errores de substitución en reconocimiento. Si no se permiten los errores de inserción ni de borrado los problemas de estocasticidad se simplifican grandemente. Si consideramos que las probabilidades de inserción y borrado son nulas (y por lo tanto ignoramos sus respectivas frecuencias), se podrán obtener las probabilidades de deformación con el procedimiento usual. Para las m reglas A->xkBk; k=1..m:
ps(b|xk) = ; pb([epsilon]|xk) = 0; pi(b|xk) =0;
Nx=
estando asegurada la estocasticidad:
Hay que notar que los heurísticos, adoptados para obtener un resultado aunque la cadena muestra sea más larga que la más larga de la gramática o más corta que la más corta (ver capítulo 6), no garantizan la estocasticidad si llegan a aplicarse ([exclamdown]equivalen a aceptar una cadena que no está en la gramática expandida!). Obviamente ello es relativamente poco importante, considerando la ya gran "informalidad" del mismo heurístico.
Los resultados comparativos entre el modelo de error completo y el de sólo sustitución, en el caso no estocástico y estocástico se muestran en el capítulo 9.
[1]Esto no es del todo cierto como se comprobará cuando se defina el tráfico y el número de caminos. en el capítulo 10.
[2] Como se verá más adelante, y debido a las particularidades del algoritmo ViterbiCorrector, el número de reglas de error es en realidad menor al presentado: todas las reglas de inserción de las reglas con el mismo no terminal a la izquierda son comunes.
[3] Modelo, por otro lado, muy utilizado en análisis sintáctico corrector de errores en gramáticas regulares.
[4] En la práctica Lni+L(Bk->xkAj) se precalculan antes de la optimización, y lo mismo podría hacerse con Li+Ts(b,[epsilon]) para utilizar directamente el -log(pi(b)).