El algoritmo de Inferencia Gramatical mediante Corrección de Errores (Error-Correcting Grammatical Inference: ECGI), es un método heurístico de inferencia gramatical, que fue diseñado en su origen para una aplicación concreta: el Reconocimiento de Palabras Aisladas. Sin embargo, las características impuestas implícitamente por ECGI (por sus heurísticos) a los lenguajes inferidos han demostrado ser comunes a muchos otros campos del Reconocimiento de Formas. Ello es debido a que ECGI intenta solventar algunos de los inconvenientes básicos que presentan, para estas aplicaciones, la mayoría de los métodos de inferencia gramatical publicados hasta el momento. Estos inconvenientes son causados por las características del extralenguaje generado por el método de inferencia, que suele ser:
* Extremadamente recursivo, lo que implica que ignora la
posición relativa de las diferentes subestructuras en la cadena muestra,
reutilizando una misma subestructura independientemente de su posición
en dicha cadena (p.e.: método uviw [Miclet,79], método
del sucesor y antecesor-sucesor [Richetin,84], lenguajes k-explorables
[García,88]).
* Infinito; lo que significa que deriva de las muestras de
aprendizaje por repetición indefinida de subestructuras de dichas
muestras (p.e.: los anteriores y también todos los métodos que se
basan en el árbol aceptor de prefijos: k-colas [Biermann,72], k-RI
[Angluin,82], método de Levine [Muggleton,84], de comparación de
finales [Miclett,80]).
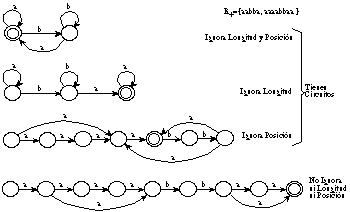
Aunque en principio estas características parezcan derivar de un procedimiento natural de generalización, tienen como consecuencia el que la gramáticas inferidas sean (figura 6.1):
1) incapaces de representar características basadas en la longitud de las subestructuras (ver apartado 1.6), pues la gramática inferida tolera longitudes arbitrarias, al no controlar el número de repeticiones de dichas subestructuras.
2) excesivamente tolerantes con las posiciones relativas de dichas subestructuras.

Todos estos procedimientos pueden verse como casos particulares de las Gramáticas de Atributos, para las cuales se ha mostrado que se puede obtener un compromiso arbitrario entre complejidad estructural (reglas) y semántica (atributos) [Fu,83].
Cabe pensar, sin embargo, que la alternativa más "limpia" se halle en un extremo de este compromiso, en el que la modelización de longitud se incluye en la misma estructura, es decir, se representa mediante la sintaxis. Este tipo de modelización admite además una solución directa, que a la vez solventa el problema de tener en cuenta la posición relativa de las subestructuras: las gramáticas no recursivas (ni a derechas, ni a izquierdas), es decir, las gramáticas sin circuitos. Lamentablemente, esta aproximación hace inaplicable la mayoría de los métodos conocidos de inferencia gramatical, lo que conduce a proponer y estudiar un nuevo algoritmo: ECGI.
El objetivo al que se destinó ECGI, desde un principio, fue el construir incrementalmente una gramática regular a partir de presentación positiva. La idea del método surgió de considerar qué mejoras serían aplicables al procedimiento más sencillo de inferencia gramatical: el que genera la gramática canónica.
Dado un conjunto finito de cadenas muestra, existe un procedimiento trivial y bien conocido para generar incrementalmente una gramática regular. Basta para ello aplicar la siguiente regla: a cada nueva muestra a=a1..an añádase a la gramática los no terminales A1..An[propersubset]N, y las reglas (S->a1A1), (A1->a2A2),...,(An-1->an)[propersubset]P (figura 6.2).
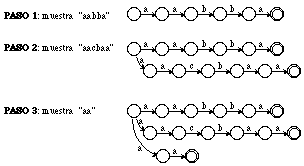
Enfocando el problema desde un punto de vista más general, si un método constructivo de inferencia gramátical M (ver capítulo 3), en un paso dado i, tiene como hipótesis, en ese paso, la gramática Gi=(Ni,V,Pi,S), entonces, para realizar la hipótesis Gi+1=(Ni+1,V,Pi+1,S) al recibir la siguiente cadena muestra ai, usualmente (puesto que es la manera intuitivamente más sencilla de ser conservativo) añadirá y/o suprimirá de Gi un conjunto, relativamente reducido (también para ser conservativo), de reglas. Como, por otra parte, los métodos existentes de inferencia en general no suprimen reglas, sino que siempre añaden reglas nuevas (debido principalmente a que sólo emplean muestras positivas y que parten de una gramática sin reglas), tiene sentido hablar del conjunto de reglas que M añade en el paso i (reglas que "no están" en la gramática de paso i), que se escribirá NEST=PihPi+1. Además, dado que, excepto en el caso de generar la gramática canónica, en NEST no están usualmente todas las reglas necesarias para generar ai, es obvio que ello quiere decir que M ha decidido que "ya existen" cierto número de reglas en Gi que permiten generar determinadas subcadenas de ai (puesto que si M es un método consistente de inferencia, Gi+1 debe poder generar ai). Con lo que, si D(ai,Gi+1)=r1,r2,...,rn; rk[propersubset]Pi+1; k=1...n; es la derivación de ai por Gi+1, entonces usualmente [existential]rk[propersubset]D(ai,Gi+1)|rk[propersubset]Pi; y podremos llamar YEST={ rk : rk[propersubset]D(ai,Gi+1) y rk[propersubset]Pi} al conjunto de reglas que "ya están" en Gi y por lo tanto no son añadidas por M al postular Gi+1.
En consecuencia, el problema principal de un método de inferencia gramatical, si quiere evitar el verse reducido a generar la gramática canónica, consiste en disponer de un método que, dada una cierta cadena muestra, le permita descubrir aquellas reglas que pertenecen a YEST (que "ya están" en la gramática).
Para ello, toda la dificultad estriba en que las cadenas muestra no llevan ninguna referencia a las reglas que las han producido, con lo que la única seguridad de que dispone un método es que dos símbolos distintos no pueden haber sido producidos por la misma regla[1]. El método ECGI, así como la mayoría de los otros métodos de inferencia gramatical, aprovechan esta certeza, e identifican grupos de reglas básicamente por similitud (según un determinado criterio, que no necesariamente implica igualdad) de las subcadenas de símbolos que generan. ECGI, además, asume que una subcadena que aparece en una determinada posición de la cadena muestra (principio, fin, centro, detrás de otra,...), no puede haber sido generada por las mismas reglas que otra subcadena, aunque sea similar, que aparezca en una posición distinta.
Por otra parte, muchos métodos de inferencia gramatical subdividen la cadena muestra en subcadenas que cumplen cierta característica (ser de una longitud determinada, terminar de una manera u otra,...) (k-colas, uviw, k-EEEI,...) y sólo entonces buscan las subcadenas en el lenguaje de la gramática para encontrar qué reglas pueden haberlas producido[2]. Lo que es más, esta búsqueda se realiza independientemente para cada subcadena. Sin embargo, ECGI busca, en el lenguaje de la gramática actual[3], la cadena más similar globalmente a la cadena muestra; aplicando un criterio de similitud de cadenas que tiene muy en cuenta la posición relativa de las subcadenas.
Una vez localizada la cadena de la gramática actual más similar a la cadena muestra, ECGI, para completar un paso de inferencia, no tiene más que asumir que las reglas que han generado subcadenas idénticas (según el criterio de similitud) en la muestra y en la cadena más similar, pertenecen a YEST (son las que "ya están"), y por lo tanto, las que pertenecen a NEST ("no están"), y que hay que añadir, son las que faltan para generar totalmente la cadena muestra.
En la práctica, para buscar en la gramática actual la cadena más similar a la cadena muestra (la fase de comparación de ECGI) se aplican los métodos de análisis sintáctico corrector de errores descritos en el capítulo 5. La derivación óptima de la cadena muestra con la gramática expandida proporciona la secuencia de reglas de error y no error, las cuales ECGI analiza en la fase de construcción, para descubrir cúales son las nuevas reglas a añadir para que la gramática acepte la cadena muestra. Las reglas de no error de la derivación óptima (reglas de YEST: que "ya están" en la gramática sin expandir) generan determinadas subcadenas de la cadena muestra, entre las cuales se hallan subcadenas generadas por las reglas de error (reglas de NEST). Para que la gramática pueda aceptar totalmente la cadena muestra, basta añadir, entre cada par de subsecuencias de reglas de YEST, un conjunto de reglas que generen las subcadenas que han sido reconocidas por las reglas de error (figura 6.3).
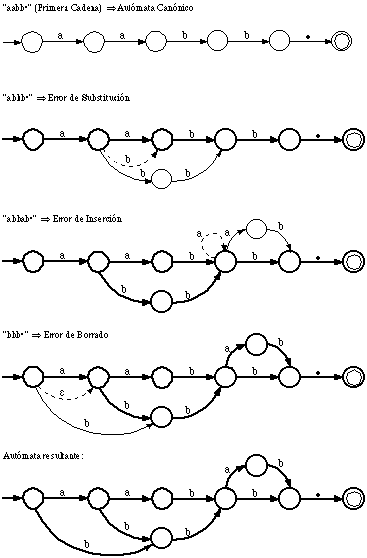
Debe resaltarse que no se añaden a la gramática las reglas de error de la derivación óptima, sino que se genera e inserta una nueva secuencia de reglas, que cumplen únicamente la condición de generar (suprimir) la subcadena de la cadena muestra ausente (sobrante) en la gramática. La nueva secuencia de reglas no sólo añade a la gramática la cadena muestra, sino tambien todas las posibles cadenas generadas por combinación de esta nueva secuencia con todas las otras antes añadidas, siendo éste el origen del poder de generalización de ECGI. Como se verá más adelante, la decisión de qué reglas exactamente se añaden, de entre las múltiples combinaciones que generarían (suprimirían) la misma subcadena, es la determinante principal de las características que son propias a todas las gramáticas que genera ECGI.
Después de lo dicho en el apartado anterior, es posible sin más preámbulos presentar formalmente el algoritmo del método de inferencia gramatical mediante corrección de errores (la relación de orden (N,<) se discute al final del apartado):
Algoritmo ECGI
Datos /* Conjunto de muestras positivas (cadenas) */
R+={ao,a1,a2,...,am}; ai[propersubset]V*
Resultado Gm=(Nm,V,Pm,S) /* Gramática regular inferida */
(N,<) /* Relación de orden en N */
Inicialización /* Gramática canónica de ao */
ao[equivalence]a1,a2,...,an
No:={ Ao,A1,...,An-1}; S:=Ao
Po:={ Ai-1->aiAi, i=1,...,n-1 } u {An-1->an}
Go:={No,V,Po,S}
(N,<):=Ao<A1<...<An-1
Inferencia
A i=1..m hacer
Comparación
Obtener /* Derivación óptima de ai en Gei */
D(ai,Gi)[equivalence]r1,r2,...,rk; rj[propersubset]Pei; j=1...k
Construcción
A rs,rs+1,...,rt-1,rt[propersubset]D(ai,Gi)
tales que rs,rt[propersubset]Pi /* NO son de ERROR */
[logicaland] rs+1,...,rt-1[reflexsubset]Pi /* SON de ERROR */
hacer
sea
rs[equivalence](Cs-1->csCs); rt[equivalence](Ct-1->ctCt)
xi[equivalence]c1,...,cs,[omega],ct,...,cl; [omega][equivalence]z1...zh
(Ni,<)[equivalence]S<...<Cs<...<Ct<...
si [omega]=[lambda]
entonces
Pi+1:=Pi u { (Cs->ctCt) }
sino
Pi+1:=Pi u { (Cs->z1Z1),(Z1->z2Z2), ...(Zh-1->zhZh),(Zh->ctCt) }
Ni+1:=Ni u { Z1,...,Zh }
(Ni+1,<):=S<...<Cs<...<Z1<...<Zh<...<Ct<...
finsi
finpara
finpara
fin ECGI
En el algoritmo aparecen bien diferenciadas las dos etapas, "comparación" (en la que se busca la derivación óptima mediante análisis sintáctico corrector de errores) y "construcción". Se comprueba, como ya se dijo en el apartado anterior, que el algoritmo de construcción genera y añade una secuencia de reglas totalmente nueva, diferente de las reglas de error propias a la derivación óptima. La construcción no aprovecha no terminales que pudieran estar en las reglas de error (en una sustitución por ejemplo) y ni siquera los tiene en cuenta para escoger qué reglas añadir. Sólo se preocupa de enlazar (dentro del si-entonces-sino) con las reglas de no error a cada extremo de la nueva subcadena que debe generar la gramática.
La complejidad del algoritmo se encuentra en su casi totalidad concentrada en el análisis corrector de errores necesario para obtener la derivación óptima. Ya se ha visto que esto supone, para cada cadena ai de longitud |ai|=n, un coste temporal O(n.|Q|.B) y un coste espacial O(n.|Q|); donde B=Bo.(2.|V| +1) debido al modelo de error utilizado. Bo (branching factor o número de reglas promedio con el mismo no terminal a la izquierda) depende de la complejidad de la gramática inferida.
Hay que notar la especial precaución que se ha tenido, a la hora de añadir no terminales, en construir y conservar un orden en el conjunto de los mismos. Recuérdese (capítulo 5) que este orden es fundamental para poder realizar en análisis corrector de errores con el algoritmo ViterbiCorrector y no tener que recurrir a Cíclico. Se consigue un orden que evita el que un no terminal se pueda derivar de uno que sea anterior a él, simplemente (y siempre que no haya circuitos) insertando los nuevos no terminales en cualquier lugar entre los no terminales Cs y Ct de la primera y última reglas añadidas. Cs y Ct pertenecen a reglas de no error, y por lo tanto, existen ya en la gramática y están correctamente ordenados. En la práctica, los nuevos no terminales se insertan justo antes de Ct.
A partir de la descripción del algoritmo ECGI, es inmediato extraer algunas de las propiedades comunes a todas las gramáticas que infiere. Es evidente, pues, que si una gramática ha sido inferida mediante ECGI a partir de un conjunto de muestras R+:
* Su lenguaje contiene a R+.
* Es regular.
* Es no determinista (aunque, como se verá en el
capítulo 12, puede conseguirse que sea determinista).
También, menos evidentemente, y como se irá justificando más adelante:
* Es ambigua.
* No tiene circuitos.
* El lenguaje que genera es finito.
Y debido a la implementación realizada:
*Es representable mediante un autómata de estados etiquetados (LAS,
ver capítulo 2).
De la descripción realizada en el apartado anterior, es posible deducir que dada la gramática actual del paso i de inferencia Gi, la cadena muestra a en ese paso, y la cadena [beta][propersubset]L(Gi) más similar a a, en ECGI se hacen las siguiente asunciones:
1) Todas las reglas que han servido para generar a, que no son de error, son reglas que han servido para generar [beta]. Es decir, Ark[propersubset]D(a,Gi+1), rk[propersubset]YEST <=> rk[propersubset]D([beta],Gi).
2) De las reglas que han servido para generar [beta] por G, sirven para generar a todas aquellas que generen subcadenas de a similares (en un sentido a definir) a subcadenas de [beta], que se hallen en la misma posición relativa en a y [beta]. Es decir, sea una descomposición arbitraria de a en n subcadenas [omega]k[propersubset]V*; k=1...n; a=[omega]1[omega]2...[omega]s...[omega]t...[omega]n; y una de [beta] en m subcadenas [Greekj]k[propersubset]V*; k=1...m; [beta]=[Greekj]1[Greekj]2...[Greekj]u...[Greekj]v...[Greekj]m; [Greekj]k[propersubset]V*; k=1...m; sea Simil([omega],[Greekj]):V*xV*->B una función que devuelve "verdad" si [omega] y [Greekj] son similares, y R[Greekj]l=r1,...,r|[Greekj]l| la secuencia de reglas que ha servido para generar la subcadena [Greekj]l de [beta], entonces, dadas un par de subsecuencias [Greekj]u,[Greekj]v[propersubset][beta]; u<v; entonces R[Greekj][propersubset]YEST [logicaland] R[Greekj][propersubset]YEST<=> [existential][omega]s,[omega]t; s<t : Simil([omega]s,[Greekj]u) [logicaland] Simil([omega]t,[Greekj]v).
Estas dos asunciones constituyen el heurístico principal de ECGI, y junto con el procedimiento de búsqueda mediante programación dinámica (corrección de errores), caracterizan a ECGI como algoritmo de inferencia gramatical.
De la primera asunción se deduce inmediatamente el corolario (figura 6.5):
C.1: Ninguna regla de la gramática actual, distinta de las que han participado en la generación de [beta], puede pertenecer a YEST.
y de la segunda asunción:
C.2: Si en a y [beta] hay dos subcadenas similares, no es posible que no hayan sido generadas por las mismas reglas (si están en la misma posición relativa).
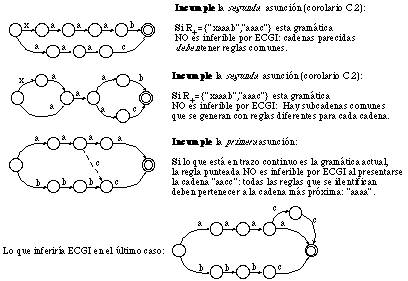
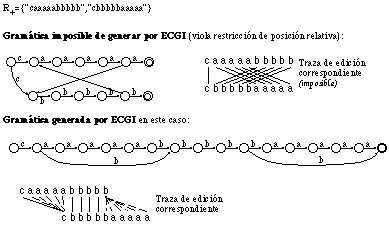
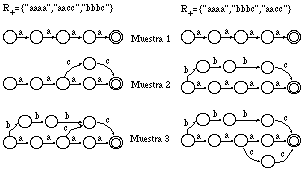
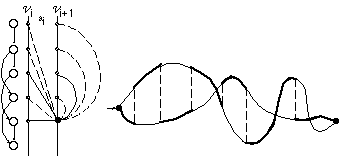
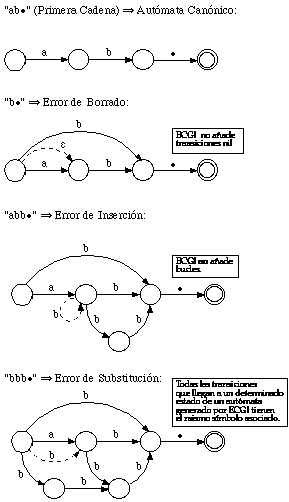
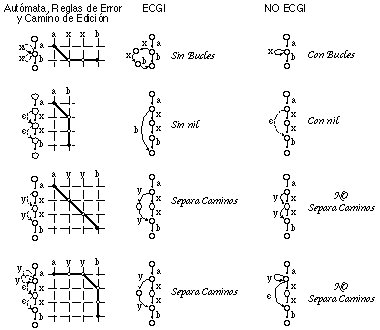
Utilizando la representación gráfica, es posible comprobar inmediatamente el porqué no se añaden sin más en la gramática las reglas error (ni derivaciones directas de ellas): ello provocaría la aparición de bucles (reglas de inserción), de reglas con el símbolo nil (reglas de borrado) o de secuencias de ellas, así como de una no separación de caminos diferentes (no se separarían los no terminales correspondientes a secuencias de reglas que generan subcadenas completamente distintas), todo lo cual se puede observar en la figura 6.9.
Dada la naturaleza no caracterizable, y por lo tanto eminentemente práctica de ECGI, es conveniente examinar hasta qué punto su proceso de inferencia es adecuado (en el sentido de que infiere estructuras "intuitivamente" correctas y adecuadas a los problemas a resolver), teniendo en cuenta las restricciones impuestas por el método y los heurísticos de construcción. Este examen además nos permitirá tomar conciencia de otro conjunto de heurísticos implícitos en ECGI.
Para el análisis se irán considerando distintos problemas de inferencia en orden creciente de complejidad, estudiándose el comportamiento de ECGI en cada caso. En cada problema se examinará la derivación óptima, analizando el camino o la traza de edición entre la cadena más próxima y la nueva cadena, y comprobando si las reglas que esta derivación induce en la construción son o no adecuadas.
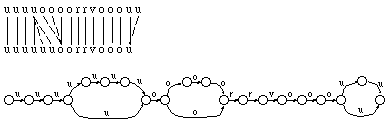
En el caso más sencillo, las dos cadenas están formadas por la misma secuencia de terminales diferentes, pero que se repiten más o menos en una u otra cadena. En la figura 6.10 se muestra un ejemplo, junto con la traza de edición y la construcción correspondiente por parte de ECGI.
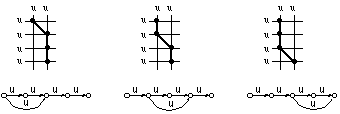
Por otra parte, en la figura 6.11 se comprueba que, aún en este caso sencillo, la derivación óptima queda indefinida: hay más de una derivación que conduce al mismo número de errores. Se representan cuatro posibles caminos de edición (en trazo grueso en el trellis) para dos cadenas: "uuuu" y "uu":
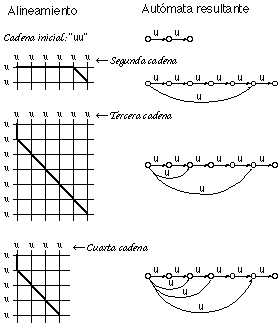
El caso de mayor dificultad ocurre cuando en un segmento de la cadena se han suprimido algunos símbolos y se han insertado otros nuevos. Ello produce una ambigüedad sobre el lugar a insertar la nueva subcadena: ¿antes, después, en medio, o en paralelo con la subcadena que se ha borrado? (ver figura 6.13).
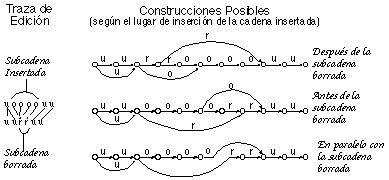
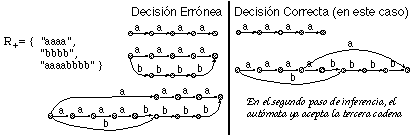
En resumen: En caso de borrado e inserción simúltáneos en un punto, ECGI procede a la inserción de la nueva subcadena en paralelo con la borrada.
En general, ECGI, al realizar el análisis de una derivación óptima se encontrará con una serie de casos de borrado, inserción y substitución de una subcadena. En lo que sigue nos centraremos en los casos de borrado, ya que los casos de inserción son simétricos a éstos, y el caso de substitución de una cadena por otra ya se ha visto en el apartado 6.5.3.2. Siempre que se produce un borrado, la subcadena borrada [omega] se encontrará entre entre otras dos subcadenas [Greekj]1 y [Greekj]2. Los distintos casos con los que se encontrará el algoritmo de construcción se definen en función de la igualdad o no de los terminales que componen [omega], [Greekj]1 y [Greekj]2. Los casos posibles serán entonces [Greekj]1[omega][Greekj]2 = uuu, unu, urr, y unr; donde cada trío define los símbolos que componen la subcadena correspondiente (p.e.: unu quiere decir que entre dos subcadenas compuestas por terminales u, se borra una subcadena compuesta por terminales distintos n). Entonces, el caso uuu (borrado de una subcadena entre dos subcadenas compuestas por los mismos que terminales que ella) es el caso sencillo, considerado en el apartado 6.5.3.1, y los otros tres casos restantes son los que se muestran en la figura 6.15, junto con la decisión que tomará la etapa de construcción de ECGI en cada uno de ellos, a la hora de decidir qué reglas debe añadir.
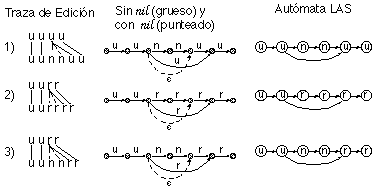
Aunque nada obligue a ello, en todas las implementaciones actuales de ECGI se ha recurrido a un único modelo de error: el descrito en el capítulo 2 para gramáticas regulares y que autoriza la inserción, borrado y/o sustitución de un símbolo en cualquier lugar de la cadena. Como también se vio en el mismo capítulo, es posible definir a partir de este modelo de error, múltiples criterios de (di)similitud entre cadenas, similares todos ellos, pero que a la hora de un análisis sintáctico corrector de errores conducen a derivaciones óptimas que pueden ser muy diferentes. Por otra parte:
* No todos estos criterios son minimizables óptimamente mediante
programación dinámica (ViterbiCorrector, capítulo 5),
aún restrinjiéndose a las definibles a partir de un modelo de
error tan sencillo como el utilizado.
* El coste de la optimización (búsqueda de la
derivación óptima) puede depender fuertemente del criterio
utilizado (el coste de ViterbiCorrector es O(|Q|.n.B), siendo la
operación elemental el cálculo de un elemento de (di)similitud y
su comparación).
Tres son los criterios que se han estudiado en este trabajo para definir la (di)similitud entre una cadena a y la gramática G, en función del número de reglas de error y no error de la derivación óptima:
minE: similitud(a,G) = Número de reglas de error.
minEL: similitud(a,G) = Número de reglas de error / Número de reglas utilizadas.
maxA: disimilitud(a,G) = Número de reglas de no error (de aciertos).
El criterio minE es el más intuitiva: una cadena se parece tanto más a otra cuantos menos modificaciones (errores) son necesarios para pasar de una a otra. Como se mencionó en el capítulo 2, este criterio es el que comúnmente se utiliza en corrección de errores, con el nombre de distancia de Levensthein, y es el que se utilizó en las primeras versiones de ECGI
El criterio minEL pretende mejorar el anterior, teniendo en cuenta las características del habla (la "elasticidad" de ciertos sonidos), aunque resulta ser una mejora aplicable a muchos otros problemas. Viene a decir: lo que importa es número relativo de errores con respecto a la longitud de la derivación. Ello puede resultar adecuado, o no, según la aplicación considerada (ver figura 6.16). El criterio minEL se utilizó en todos los experimentos de ECGI, excepto en los últimos correspondientes al reconocimiento de imágenes.
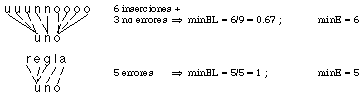
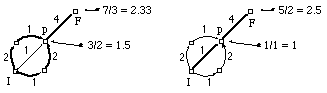
El criterio maxA se deriva de la observación de que la etapa de construcción de ECGI se basa única y exclusivamente en las reglas no erróneas. ECGI genera tantos menos no terminales y reglas, cuantas más reglas no erróneas haya en la derivación (para una longitud de muestra dada), puesto que añade una regla por cada símbolo de la muestra que no ha podido ser generado por una regla de no error. En teoría, pues, el criterio maxA debe llevar a ECGI a generar menos reglas, y ello independientemente del problema considerado. Es el criterio que se utilizó en la tarea de reconocimiento de imágenes.
Sin embargo, a pesar de que en principio genere menos estados, la maximización de aciertos no impide que, en algún caso, se produzcan efectos indeseables que una normalización por la longitud de la derivación, o una minimnización de errores, hubieran evitado (ver figura 6.18).
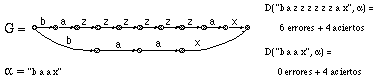
Intuitivamente se plantea de inmediato la duda de si las distancias expuestas anteriormente son o no equivalentes; especialmente, si no será lo mismo minimizar el número de errores que maximizar el número de aciertos. En este apartado examinamos la relación formal existente entre estos y otros criterios.
Sea L, E, A respectivamente el número de reglas, el número de reglas de error y el número de reglas de no error de una derivación. Los criterios a considerar se obtienen evaluando (d es una derivación cualquiera):
minE =
minEL =
maxA =
Comparando el criterio minE con el maxA, se comprueba inmediatamente que no es lo mismo minimizar errores que maximizar aciertos. En efecto, para toda derivación, se cumple L=E+A, y para dos derivaciones distintas 1 y 2:
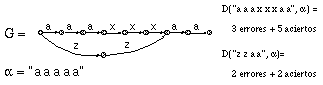
Debe observarse que ninguno de los criterios definidos en los apartados anteriores lleva a cabo una alineación perfecta de las cadenas (en el sentido más intuitivo), si se asume la "elasticidad" de las subcadenas. En concreto, todos estos criterios asumen que resulta igual de costoso insertar (borrar, por simetría) el mismo símbolo ya presente que uno completamenta distinto, tal como se comprueba en la figura 6.20. Asimismo, se observa en la misma figura que, ECGI, en el caso más intuitivo, agruparía en subredes los segmentos más parecidos, al contrario de lo que hace la presente versión. Sin embargo como también se ve, ello conllevaría un incremento en el número de reglas añadidas.
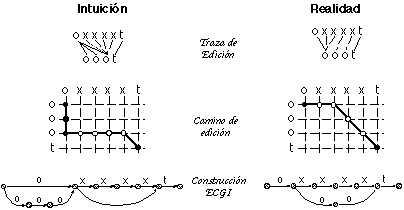
Finalmente, para evaluar los tres criterios de (di)similitud aquí considerados, desde el punto de vista de su eficacia y adecuación para ECGI, se han realizado una serie de experimentos de reconocimiento de formas, que se presentan en el capítulo 9.
Las gramáticas, se hayan obtenido o no mediante un método de inferencia a partir de un conjunto de muestras, pueden aplicarse de diversas maneras al reconocimiento de formas (modelización de conocimientos linguísticos, traducción, clasificación, etc...). De entre todas estas maneras, la más sencilla consiste en emplear las gramáticas como clasificadores.
Toda gramática representa (genera) un lenguaje, y siempre existe un reconocedor de las cadenas de ese lenguaje asociado a la gramatica. En los casos más sencillos, las gramáticas regulares, ese reconocedor es un autómata finito. Un autómata se comporta realmente como un reconocedor de formas: dado un objeto (una cadena) es capaz de decidir si ese objeto pertenece o no a la forma que representa: el lenguaje de la gramática. Nada impide utilizar las gramáticas inferidas por ECGI aplicando esta idea, reduciéndose entonces la operación de reconocimiento a un análisis sintáctico, con una decisión final si/no de pertenencia al lenguaje. Sin embargo, y como ya se ha mencionado en el capítulo 2, esta aproximación, aunque sencilla, es poco factible en la práctica.
La razón de esta infactibilidad se halla cuando se constata que las gramáticas inferidas por ECGI, en un caso real, no modelizan la totalidad del lenguaje que tienen la misión de reconocer. Ello es debido, principalmente, a que la presentación de ejemplos nunca puede ser completa. En concreto, en las tareas mínimas de reconocimiento de formas planteadas a ECGI, existen dos fuentes principales de variabilidad en las cadenas del lenguaje buscado, que limitan seriamente la completitud del conjunto de muestras R+:
* El "ruido", que altera las cadenas introduciendo una serie de errores
más o menos aleatorios. Estos errores inducen una variabilidad casi
ilimitada, que impide toda convergencia final del aprendizaje, al ser muy alta
la probabilidad de que aparezca un error, aún no modelizado por no
hallarse presente en R+.
* Las variaciones de longitud de las subestructuras, que es casi imposible
que se den en toda su variedad en R+.
Es pues obvio que la inferencia debe detenerse en un punto razonable, en el que las principales características estructurales de R+ han sido registradas, junto con los errores (debidos o no al ruido) más frecuentes y las variaciones de longitud más usuales. Un criterio razonable de detención de la inferencia en estos casos podría ser esperar a que la distancia promedio a la gramática de las últimas (n) muestras baje por debajo de un umbral[4].
Por otra parte, si se detiene el aprendizaje antes de que la gramática inferida genere la totalidad del lenguaje buscado, es evidente que es imposible utilizar sin más dicha gramática (su autómata) en reconocimiento, pues muchas cadenas que deberían ser aceptadas no pertenecen al lenguaje inferido. En reconocimiento sintáctico de formas, la solución que usualmente se da a esta dificultad, tal como se mencionó en el capítulo 2, consiste en extender la gramática inferida recurriendo a métodos de análisis sintáctico corrector de errores. Esta aproximación cuenta con la ventaja de que la gramática inferida sólo tendrá que dar cuenta de las características estructurales más importantes, y como mucho, de los errores más probables, puesto que el modelo de de error (el que se emplea en reconocimiento, no confundirlo con el que emplea e ECGI en inferencia) da cuenta de los errores y/o variaciones menores.
Concretando todas estas consideraciones:
1) En los experimentos llevados a cabo para este trabajo, se han utilizado las gramáticas inferidas por e ECGI como clasificadores de dígitos (hablados, manuscritos e impresos) o letras (habladas).
2) Cada forma (dígito) se ha representado mediante una única gramática, inferida por ECGI.
3) El reconocimiento se efectúa mediante un análisis sintáctico corrector de errores de la muestra por cada una de las gramáticas inferidas, lo que proporciona un conjunto de (di)similitudes muestra-gramática. Para la decisión, se recurre a la regla del vecino más próximo (NN) [Duda,73], en su versión más sencilla: se escoge aquella clase cuya distancia a la muestra sea mínima (o cuyo parecido sea máximo).
Por otra parte, como se verá en el capítulo 7 ("extensión estocástica del ECGI"), es posible almacenar la información estadística asociada a la frecuencia de utilización de las reglas, de manera que las gramáticas inferidas por ECGI sean estocásticas. En este caso, el análisis sintáctico corrector de errores será también estocástico, y para la decisión se aplicará la regla de máxima verosimilitud (basada en la regla de Bayes [Duda,73]): se escoge la clase que maximiza la probabilidad de pertenencia de la cadena a la gramática.
Dada la naturaleza absolutamente incremental del proceso de aprendizaje de ECGI, es perfectamente factible implementarlo de manera que simultánee el reconocimiento de la nueva muestra y su aprendizaje, permitiendo la evolución del modelo inferido aún cuando ya está en plena utilización.
Por otro lado, a cada nueva cadena muestra, el primer paso del algoritmo de inferencia de ECGI consiste en obtener la derivación óptima de la muestra con respecto a la gramática actual. Nada impide que el análisis sintáctico corrector de errores, que supone el buscar esta derivación, proporcione al mismo tiempo una (di)similitud muestra-gramática utilizable para el reconocimiento de la misma. Ello autoriza una integración de los procesos de inferencia y reconocimiento, que no sólo resulta conceptualmente atractiva, sino que permitiría reducir fuertemente el coste computacional en caso de utilizarse ECGI en una aplicación que requiera aprendizaje continuo.
El siguiente algoritmo ilustra este proceso continuo de aprendizaje y la posible reducción de coste computacional mediante integración inferencia-reconocimiento. En él, un operador solicita la realización de una tarea mediante presentación de una forma representada por la cadena a. ECGI efectúa un reconocimiento, presenta la forma reconocida y solicita confirmación. Si la respuesta proporcionada por el operador es positiva, ECGI efectúa la tarea solicitada e integra la nueva cadena a la gramática inferida para la clase reconocida. Si la respuesta es negativa, se solicita al operador cuál es la clase correcta (mediante un medio más seguro), y se actualiza la gramática de esa clase, obviamente, después de haber de realizado la tarea solicitada. El proceso es en principio indefinido, y se detiene sólo cuando el operador ya no tenga más tareas que realizar:
Algoritmo Integración
Datos M /* número de clases a reconocer */
Goi i=1..M /* M gramáticas iniciales */
Método
hacer indefinidamente
Aceptar una nueva muestra a
/* Análisis sintáctico corrector de errores */
Obtener D(a,Gi) y /* Derivación óptima y */
dist(a,Gi) i=1...M /* disimilitud a,Gi */
Postular clase de a:=k=
Solicitar confirmación /* al operador */
si correcto
entonces
Realizar Tarea(k)
construcción(Gk,D(a,Gk))
sino
Solicitar t=clase correcta
Realizar Tarea(t)
construcción(Gt,D(a,Gt))
fin si
fin hacer
fin Integración
En esta óptica, se entrena inicialmente el sistema -por ejemplo, utilizando el mismo algoritmo, pero sin efectuar el paso "Realizar Tarea" las N primeras veces (N reducido~30)- con relativamente pocas muestras, aprovechando la rápida convergencia inicial de ECGI. Seguidamente se entra en fase de producción, dejando que el refinamiento posterior, mucho más lento, se haga durante la utilización. Esto no sería excesivamente molesto para el usuario (la tasa de reconocimiento fácilmente superaría el 80% en un principio), con la ventaja de disponer en todo momento de una adaptación a las circunstancias (cambio de locutor, de útil de escritura, catarro, etc.).
Dos observacions adicionales, en caso de plantearse una aproximación mediante Integración:
* Sería imprescindible una simplificación periódica de
los autómatas (gramáticas) inferidos, para evitar un crecimiento
indefinido (ver capítulo 10).
* El modelo de corrección de errores y el algoritmo de
análisis sintáctico deberían ser el mismo en
comparación y reconocimiento; en caso contrario se pierde la ventaja
computacional, aunque se puede seguir aprovechando la capacidad de aprendizaje
incremental de ECGI.
Se ha subrayado que ECGI (lo mismo que cualquier algoritmo de inferencia gramatical cuando trata muestras ruidosas y distorsionadas), infiere no sólo la gramática buscada, sino también un modelo de los errores más frecuentes (probables) que se producen en las muestras. El papel del modelo de error aplicado en reconocimiento es únicamente el de dar cuenta de aquellos errores imposibles de inferir por su poco significado estructural y su infinita variedad.
Por otro lado, si no se opta por una aproximación integradora de la inferencia y el reconocimiento, es posible aplicar modelos de error totalmente distintos en aprendizaje y reconocimiento. Dado que en reconocimiento suele requerirse un mínimo coste computacional, cabe pensar en utilizar durante esta fase un modelo de error menos costoso. Si se recuerda que el coste del algoritmo de reconocimiento es estrictamente el de ViterbiCorrector, O(n.|Q|.B), con B dependiendo directamente del número de reglas aplicables a cada no terminal, una reducción drástica en el número de las reglas de la gramática expandida se obtiene autorizando únicamente errores de sustitución. El número de reglas por cada regla de la gramática no expandida se reduce en más de la mitad (de 1+2.|V| a |V|).
Pero la ventaja computacional que se obtiene, autorizando únicamente errores de substitución, no sólo es debida a la reducción en el número de reglas de la gramática expandida. Desarrollos recientes de ECGI [Torró,90] [Alfonso,91], que utilizan técnicas subóptimas para reducir drásticamente (a menos de un 10% de la original) la complejidad temporal de un reconocimiento, sólo son posibles si no se autorizan las reglas de borrado.
En la práctica, autorizar tan sólo sustituciones al efectuar la búsqueda de la cadena más similar en la gramática, equivale a suprimir toda posibilidad de estiramiento o compresión de las subcadenas de la muestra con respecto a las muestras de aprendizaje. Puesto que se está suponiendo que la gramática inferida modeliza suficientemente los errores más probables que se producen en las muestras, se espera que esto no resulte una penalización excesiva para la eficacia del reconocimiento; esperanza que se ve confirmada por la experiencia, como demuestran los resultados resumidos en el capítulo 9. Desde luego, llevando la idea hasta un extremo, podría pensarse en suprimir totalmente el modelo de error en reconocimiento; pero en este caso, como ya se ha hecho notar anteriormente, un error, por mínimo que sea, provocaría el rechazo inmediato de la cadena. Por otra parte, existe una posibilidad incluso menos drástica que la de autorizar tan sólo sustituciones, y que consiste en sólo prohibir las reglas de borrado. Esta aproximacíon, que reduciría a |V|+1 en vez de a |V| el número de reglas, no se ha considerado, al resultar, en principio, satisfactorios los resultados obtenidos con sólo substituciones.
La variabilidad en logitud tolerada cuando sólo hay sustituciones está limitada por la longitud de las cadenas más larga y más corta generables por la gramática. Ello, si no se toman precauciones, provoca, o bien el rechazo (si la implementación lo tiene previsto), o bien la obtención de resultados incoherentes; esto último debido a que la búsqueda en el trellis se detiene inesperadamente en uno de sus lados: se acaba la cadena y no se llega a un estado final, o todos los caminos posibles han llegado a un estado final sin haber llegado al final de la cadena.
En esta implementación, para evitar el rechazo y obtener a pesar de todo resultados coherentes, se han adoptado las dos reglas siguientes:
* Si una cadena es más larga que la máxima generable, se
trunca.
* Si una cadena es más corta que la mínima generable, la
distancia final es la del estado alcanzado que tenga la mínima distancia
al detenerse la búsqueda (basta para ello buscar el nodo con la
distancia acumulada mínima en la última columna del trellis).
Estas reglas suponen implícitamente que la parte final de una cadena muy larga no contendrá información esencial para poder decidir a qué clase pertenece (lo cual es usualmente cierto), y para aplicarlas es necesario conocer la longitud de las cadenas más corta y más larga, ambas obtenibles mediante los algoritmos detallados en el capítulo 10.
Desde un principio, se adoptó para ECGI una representación no convencional de las gramáticas regulares inferidas. Esta representación, en forma de autómatas de estados etiquetados (LAS: labelled states automata, ver capítulo 2) fue impuesta inicialmente por razones de facilidad de implementación, ya que permite una cómoda visualización de la derivación óptima y una representación gráfica sencilla de los autómatas inferidos; aunque posteriormente se comprobó, como se explica en el apartado 6.5.3.3, que en algunos casos conduce a generalizaciones más acordes con la intuición. Resumiendo: ECGI infiere (en la presente implementación) autómatas de estados etiquetados (LAS).
Por otra parte, para no tener que trabajar con multitud de estados finales y para conseguir que la búsqueda de la derivación óptima consista realmente en la búsqueda del camino mínimo entre sólo dos vértices del trellis, en la implementación de ECGI se ha definido un símbolo final (*). De esta manera: en los autómatas que infiere, ECGI añade, para cada estado final del LAS qa, una transición (qa,*,q*), que va de ese estado a un único estado final q*, etiquetado con *. En estas condiciones, para que la condición de reconocimiento se siga cumpliendo, resulta necesario añadir el símbolo final a todas las cadenas a reconocer por el autómata. Además, por simetría, para simplificar la implementación y no tener que tratar de modo especial al estado inicial, se añade también a las cadenas el terminal correspondiente al estado inicial: ~. Esto no altera los autómatas inferidos, pero implica modificar la definición dada en el capítulo 2, de <<lenguaje reconocido por un LAS>>, puesto que se supondrá que el símbolo inicial es reconocido por el estado inicial qo. Con esta modificación, el lenguaje reconocido por un autómata LAS de ECGI, inferido para la gramática G, será (figura 6.21):
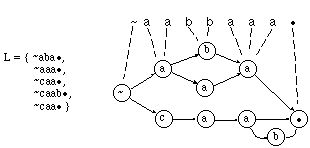
Aprovechando que un LAS tiene etiquetados los estados, y que los autómatas inferidos por ECGI no tienen circuitos, lo cual permite ordenar los estados topológicamente, es posible una visualización muy descriptiva de dichos autómatas:
Para representar un LAS inferido por ECGI se dibuja un eje de estados (horizontal) 1..|Q| donde 1 es el primer estado y |Q| el último. Perpendicularmente a este eje, se coloca otro eje en el que figuran los terminales 1..|V|, donde |V|-1 es el primer terminal y |V| es el último. Los restantes símbolos se ordenan de manera que los símbolos más similares (según la física del problema o cualquier otro criterio adecuado) estén más cerca. En estas condiciones, cada estado qi, de número de orden i (según el orden topológico), viene representado por un punto (i,eti(qi)) (recuérdese que eti(qi) es la etiqueta -terminal- asociado al estado), y las transiciones se pueden dibujar como rectas que unen los estados. La representación asegura que no hay dos estados en la misma vertical, con lo que únicamente pueden confundirse las transiciones que van entre dos estados con el mismo símbolo. Por otra parte, la confusión que es fácilmente evitable si se dibujan estas transiciones curvadas (aunque no se ha hecho en este trabajo).
Un dibujo de este tipo (véase un ejemplo en la figura 6.22) permite visualizar muy bien la estructura inferida, poniendo en relieve su linealidad, así como las secuencias de estados que representan subestructuras o subcadenas formadas por los mismos símbolos o similares (que corresponden a varios estados seguidos en la misma horizontal o próximos a ella).
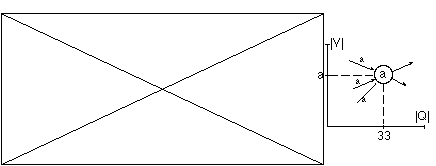
El cambio de representación que suponen los LAS, aunque no afecta a la filosofía de ECGI, influye fuertemente en su implementación. En particular, el algoritmo de construcción adquiere un aspecto distinto, que es conveniente exponer.
El algoritmo, tal como se muestra a continuación, es una transcripcción literal del utilizado en la práctica, y por lo tanto, trata con un autómata LAS y no con una gramática. La principal diferencia, con respecto a la versión presentada previamente, reside en que se ha explicitado el algoritmo de análisis de la derivación óptima, así como las comprobaciones que se realizan sobre esta para detectar las reglas de no error. En efecto, el algoritmo de análisis sintáctico corrector de errores proporciona la derivación óptima como una secuencia de vértices del trellis p=(q,a)[propersubset]QxV, es decir, como una función pred:QxV->QxV, asociada a cada vértice p[propersubset]QxV, que da el siguiente vértice del trellis según la derivación. Para detectar una regla de inserción (A->aA), basta comprobar que el no terminal (el estado) es el mismo en ambos lados de la regla; es decir, hay que comprobar en la derivación que, al pasar de un vértice de la derivación (q,a) al siguiente (q1,a1), no cambia el estado asociado a dichos vértices, o sea que q=q1. Para ello se define la función q:QxV->Q, que al ser aplicada a un vértice (q,a)[propersubset]QxV proporciona q[propersubset]Q. Similarmente, una regla de borrado puede detectarse comprobando que no cambia el terminal asociado a dos vértices del trellis, consecutivos según la derivación (o sea a=a1), para lo cual se define la función v:QxV->V que dado (q,a)[propersubset]QxV, proporciona a[propersubset]V. Finalmente, en una regla de sustitución cambian tanto el estado como el terminal (q!=q1, a!=a1), siendo una regla de no error si además la etiqueta del estado (proporcionada por la función eti:QxV->V) es igual al primero de los terminales (es decir, a) (recuérdese que el autómata es un LAS).
En la práctica, no es necesario comprobar si el terminal o el estado cambian al pasar de un vértice a otro del trellis. El algoritmo de análisis corrector de errores, proporciona la información sobre tipo de regla de error de la que se trata en cada vértice del trellis. Para detectar una regla de no error, basta entonces comprobar sólo si la etiqueta del estado asociado al vértice es igual al terminal asociado al mismo. Sin embargo, la explicación anterior será útil para entender, tanto el algoritmo ECGI-AS, como su verisón modificada, que se presenta un poco más adelante.
Algoritmo ECGI-LAS (construcción)
Datos Gi /* Gramática actual */
ai /* muestra */
D(ai,Gi) /* Derivación óptima de xi en Gi */
Resultado Gi+1 /* Gramática inferida */
Auxiliar /* las 3 primeras son funciones sobre un vértice del trellis */
q:QxV->Q /* estado asociado */
v:QxV->V /* terminal asociado */
pred:QxV->QxV /* vértice anterior según D */
eti:Q->V /* etiqueta de un estado (LAS) */
Variables
p,pu[propersubset]QxV /* vértice examinado y último vértice en
que se ha identificado */
Inicialización
p=(q*,*); pu=p; /* Se comienza desde el último punto del trellis */
Método
mientras p!=(qo,~) hacer
p=prev(p) /* Se toma el siguiente vértice */
si v(p)=eti(q(p))
entonces /* Puede no ser error */
sea ai=b1...bs[beta]bt...bl;
donde bs=v(p); bt=v(pu); [beta]=z1...zh; bi,zi[propersubset]V,Ai
si TipoRegla(p,pred(p))=Substitución
entonces
si ai=[lambda] entonces
si no existe ya, crear (q(p),bt,q(pu))
sino crear
qz,qz,...,qz
(q(p),z1,qz),(qz,z2,qz),...,(qz,bt,q(pu))
pu=p
fin si
fin si
fin si
fin mientras
fin ECGI-LAS (construcción)
Obsérvese la variable "pu", que permite recordar en qué vértice del trellis se ha encontrado la última regla de no error.
Aún sin ser necesario, se ha explicitado el sentido de recorrido de la derivación óptima, de atrás hacia delante, como recordatorio de cómo se ha realizado la implementación actual y de cómo se obtendría si se aplica el algoritmo ViterbiCorrector tal como se ha expuesto. Es posible, sin ningún coste adicional, evaluar los sucesores en vez de los predecesores en cada vértice del trellis [Torró,89], con lo que se podría recorrer la derivación empezando desde el primer estado en vez del último.
Se ha prescindido de los detalles del algoritmo destinados a preservar el orden en el conjunto de estados. La regla es exactamente la misma que en el caso de la gramática y consiste simplemente en insertar los estados antes de q(pu).
Es posible visualizar muy sencillamente el proceso de construcción en un LAS, representándolo sobre el camino de edición (ver figura 6.23).
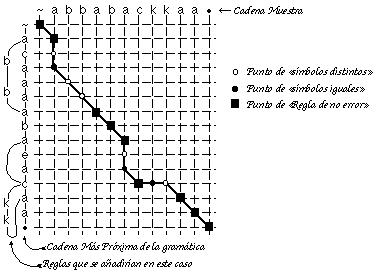
si TipoRegla(p,pred(p))=Substitución (1)
por :
si q(p)!=q(pu) y /* no pueden haber bucles */ (2)
s!=t /* no hay transición nil */
En la definición 2, se observa que no hay ninguna referencia directa al tipo de reglas (de error o no) que se analiza en cada momento. No debe creerse que esto equivale al método, explicado al principio del apartado, en el que se averigüaba el tipo de regla de error mediante comprobación del cambio de terminal o estado asociado, al pasar, en la derivación, de un vértice del trellis al siguiente. Aquí la comprobación se hace, no entre un vértice y el siguiente de la derivación, sino entre un vértice y el último vértice en el que se ha producido identificación (diremos que se produce identificación cuando el algoritmo toma las acciones correspondientes a la detección de una regla de no error en la derivación: aquí cuando v(p)=eti(q(p)) y q(p)!=q(pu) y s!=t, y en el caso original cuando v(p)=eti(q(p)) y TipoRegla(p,pred(p))=Substitución).
La definición 2, puede verse como un heurístico que modifica la definición de "identificación" para el caso de un autómata LAS, en un intento de aprovechar las características propias de estos autómatas. El comportamiento diferente de las dos definiciones se puede comprobar en la figura 6.24. Se observa que la definición 2 genera un estado menos. Nótese que la situación presentada en la figura es poco usual, máxime si se recuerda que uno de los heurísticos de ECGI otorga preferencia a la substitución.

[1] A menos que haya errores, pero en este caso supondremos que se trata de inferir, no sólo la gramática original, sino también los errores que se producen sobre ella: las "reglas de error" reales.
[2] En el caso de los métodos no incrementales, la búsqueda de subcadenas similares se realiza en el mismo conjunto de muestras de aprendizaje.
[3] En adelante, al considerar una nueva cadena muestra ai, llamaremos "gramática actual" a la gramática inferida hasta ese momento por un método incremental de inferencia, es decir, a la gramática inferida por el método a partir del conjunto de cadenas R+={a1,...ai-1}.
[4] En la práctica, debido a la perenne escasez de muestras que sufren los estudiosos del reconocimiento de formas, el aprendizaje se detienen cuando ya no quedan más muestras (nótese además que en este caso las muestras no pueden ser reutilizadas en un proceso de reestimación).