Tal como se ha mencionado en el capítulo 2, el análisis sintáctico corrector de errores involucra un paso previo, consistente en la construcción de la gramática expandida de la gramática original. Ello implica, a primera vista, no sólo una enorme multiplicación en el número de reglas a analizar, sino también un esfuerzo considerable para generarlas y un espacio no menos considerable para almacenarlas. Sin embargo, cuando se trata de gramáticas regulares (en las que nos centraremos en el resto de este trabajo), es posible fundir en un solo y único proceso la generación de la gramática expandida y el análisis sintáctico corrector de errores. Ello posible gracias a que las reglas de error son deducibles directamente de las reglas de no error, lo que permite ir construyéndolas "al vuelo".
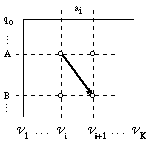
En el capítulo anterior se ha mostrado que se puede llevar a cabo el análisis sintáctico en gramáticas no deterministas buscando un camino extremal en un grafo, el trellis, construído a partir de la cadena a analizar y de la gramática (o su autómata equivalente). Utilizando la misma notación y representación que en dicho capítulo, se comprueba fácilmente el que, para una regla cualquiera de la gramática característica G=(N,V,P,S) A->aB; A,B[propersubset]N, a[propersubset]V, y el símbolo i-ésimo ai[propersubset]V de una cadena a=a1,a2,...,an; la arista que deberá considerarse, al recorrer el trellis correspondiente, será la mostrada en trazo fino en la figura 5.1 (sólo se presentan las etapas consideradas, Vi y Vi+1 y los vértices afectados por la regla en cuestión).

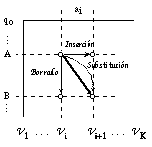
Una gramática regular (autómata) libre de circuitos es aquella en la que ninguna secuencia de reglas aplicadas a partir de un no terminal lleva a él mismo:
En efecto, para poder aplicar la versión iterativa del esquema de programación dinámica, la condición básica consiste en que, en un punto dado, todos los resultados anteriores estén calculados. En el caso del trellis, ello quiere decir que deben estar calculados todos los vértices de los cuales provenga una arista que llegue al vértice que estamos calculando. Como el cálculo progresa de etapa en etapa, es obvio que esta condición se cumple para todas las aristas provenientes de la etapa anterior, pero nada garantiza que sea cierta para aristas que provengan de vértices de la etapa que se está calculando, aristas que, como se ha visto, son inevitables si se consideran errores de borrado.
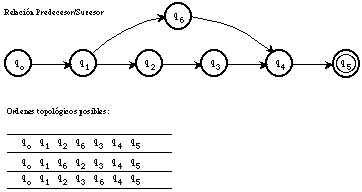
Según la definición de trellis, cada vértice corresponde a un estado q del autómata, y a ese vértice sólo pueden llegar aristas provenientes de vértices que corresponden a estados que sean predecesores[1] de q; ello independientemente de si estas aristas son debidas a transiciones normales o de error. Teniendo esto en cuenta, es evidente que, para poder utilizar el algoritmo de Viterbi considerando errores de borrado, debe de ser posible ordenar los estados del autómata (y por lo tanto, los vértices en las etapas del trellis) de manera que todos los estados predecesores de uno dado sean anteriores a él. Si este orden es factible, implica una ordenación parcial del conjunto de estados y por lo tanto, la operación subsiguiente de encontrar un orden lineal, superconjunto de este orden parcial (con el fin de ordenar en columna los estados para formar una etapa del trellis), será lo que se conoce como ordenación topológica (ver figura 5.3). Es muy sencillo mostrar [Horowitz,77] que un orden parcial (y por lo tanto topológico) en un grafo dirigido sólo es posible si éste no tiene circuitos, lo que en nuestro caso implica el que el autómata (gramática) no los tenga[2].
Algoritmo OrdenTopológico
Método
mientras haya vértices hacer
si todo vértice tiene un predecesor
entonces error: "Hay un ciclo" fin
buscar un vértice v que no tiene predecesores
escribir v
borrar v y todas las aristas que salen de v
finmientras
fin OrdenTopológico
Como ha quedado demostrado en el apartado anterior, y siempre que una gramática regular esté libre de circuitos, es posible utilizar el algoritmo de Viterbi para llevar a cabo el análisis sintáctico corrector de errores estocástico. Se presenta a continuación es una versión de este algoritmo, adaptada para esta aplicación en particular, mediante los añadidos necesarios para "generar" las reglas de error (la gramática expandida) a la vez que lleva a cabo el análisis sintáctico (algoritmo de Viterbi con corrección de errores):
Algoritmo ViterbiCorrector
Datos /* [tau] es el tipo "estado", [sigma] el "símbolo", A=(V,Q,qo,F,d) */
V:C[sigma] Q:C[tau] qo:[tau] F:C[tau] a=a1a2...an:L[sigma]
Resultado R:R
Auxiliar /* [psi] es el tipo "error" */
p:[tau]x[sigma]x[tau]->R /* probabilidad de una transición */
pe:[tau]x[psi]x[tau]->R /* probabilidad de error en una transición */
sig:[tau]->[tau] /* ordenación de estados*/
Variables P,P':C[tau]xR /* Vectores, indexados por [tau] */
q,q':[tau]
Método
Aq'[propersubset]Q hacer P'[q']:=0 finA
P'[qo]:=1;
para j:=1..|a| hacer /* Etapa del trellis */
q:=qo
repetir
P[q]:=max {
/* reglas de no error: q->aq', a=aj */
{P'[q'].p(q',aj,q)},
/* reglas de sustitución: q->ajq', a!=aj */
{P'[q'].pe(q',sa|a,q)},
/* regla de inserción: q->ajq */
{P'[q].pe(q,i,q)},
/* reglas de borrado: q->q' */
{P[q'].pe(q',ba,q)}
}
q:=sig(q)
hasta q=indefinido
P':=P
finpara
R:=
fin ViterbiCorrector
En el algoritmo se da un tratatamiento por separado a cada tipo de error, habiéndose escrito[3] la probabilidad de una transición (regla) de error entre los estados q y q' en cada caso como pe(q',sa|b,q) si es sustitución de a por b, pe(q,ia,q) si es inserción de a y pe(q',ba,q) si es borrado de a.
Puede observarse como en las reglas de borrado se utiliza el vector P (el que se esta calculando) en lugar del P'. Obviamente se ha supuesto que los estados están ordenados en el trellis según un orden topológico dado por la función "sig". El primer elemento de tal ordenación siempre será el estado inicial qo.
No es fácil encontrar en la literatura una solución completa y eficiente al problema del análisis sintáctico corrector de errores, en el caso más general de gramáticas regulares con circuitos. [Thomason,74] estudia el tema, pero no plantea una solución clara; la primera[4] solución completa parece haber sido expuesta en un trabajo muy poco conocido [Alpuente,89], y sólo recientemente [Bouloutas,91] trata el problema desde un punto de vista más general, en una exposición muy similar a la presentada a continuación, resolviendo el problema, pero sin proponer un algoritmo práctico de minimización.
Hemos visto que, en el caso de haber circuitos en el autómata, es inevitable la existencia de vértices del trellis cuyo cálculo depende de vértices no previamente calculados; es decir, que es imposible ordenar las aristas verticales (intra etapa) de manera que vayan todas en una dirección (el orden topológico); lo que implica que hay circuitos en las etapas del trellis.
El problema que se plantea es pues el de buscar el camino óptimo en la etapa de un trellis, la cual tiene circuitos, a partir de unos costes iniciales por vértice dados por la evaluación de las aristas provenientes de la etapa anterior. Obviamente, para ello se requiere un algoritmo que encuentre el camino óptimo en un grafo dirigido y ponderado con circuitos.
En lo que sigue nos situaremos en el caso de minimización del coste de un camino en el que el coste total es la suma de los costes elementales, todos positivos. Otros casos, como maximización o utilización del producto, son similares, siempre que se cumpla la condición que se discute más adelante.
La búsqueda del camino mínimo en un grafo es un problema típico de algorítmica, y su solución viene dada por el algoritmo de Dijkstra [Horowitz,77]; el cual se basa en la siguiente constatación: Un camino por un grafo ponderado, que llega a un vértice del mismo, NO puede ser el mínimo si ya ha pasado por ese vértice. Lo que resulta evidente, puesto que siempre será menos costoso la primera vez. En estas condiciones, a la hora de minimizar:
* Se pueden despreciar los bucles (aristas de un vértice a
sí mismo): un camino que pasa por un bucle pasa más de una vez
por el vértice.
* Para el resto de los circuitos en el grafo, se recorrerán las
vueltas atrás como máximo UNA vez (y una vez como mínimo
también: hay que comprobarlas).
Con lo que, para llevar a cabo la búsqueda del camino mínimo en un grafo de G=(V,A), con circuitos, se puede recurrir al siguiente algoritmo de PD:
Algoritmo MINCIRCUITOS
Datos /* [tau] es el tipo "vértice", G=(V,A) */
Co:C[tau]xR /* Vector de costos iniciales, indexado por [tau] */
Variables C:C[tau]xR /* Vector, indexado por [tau] */
HayModif:B /* Hay estados modificados */
v,v':[tau]
antes:R
Método
C:=Co
Repetir
HayModif:=falso
Av[propersubset]Q hacer
antes:=C[v]
C[v]:={C[v'] + Ce(v',v)}
si C[v]!=antes entonces HayModif:=verdad
finA
hasta no HayModif
fin MINCIRCUITOS
Donde Ce(v',v) es el peso de la arista (v',v). Este algoritmo es una versión del Dijkstra, en la que no se fuerza el vértice inicial (aunque ello se pueda conseguir simplemente inicializando a cero el coste acumulado del vértice inicial y a infinito el de los demás). Para poder determinar el vértice inicial del camino que llega a cada vértice, sería necesario anotarse en cada punto la decisión tomada; de la misma manera (ver capítulo 4) que se hace para determinar la derivación en el caso del análisis sintáctico con los algoritmos de PD.
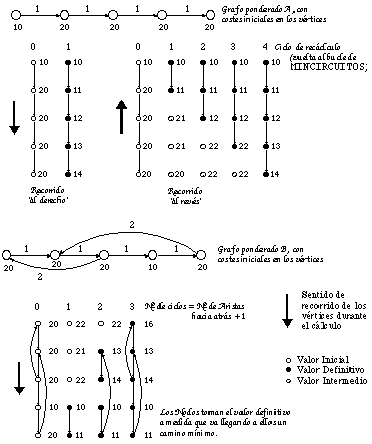
Para definir la condición de fin se aprovecha implícitamente el hecho de que el camino mínimo no pasa dos veces por un mismo vértice. En efecto, a cada vuelta del bucle los caminos progresan de un vértice y se modifican los costes de aquellos vértices que son alcanzados, si su valor precedente es mayor (ver figura 5.4). Llegará pues inevitablemente un momento en el que el camino mínimo, o bien haya recorrido todos los estados, o bien le corresponda pasar por un estado por el que ya ha pasado; como llegado ese momento no se producirá ninguna modificación de costes, se podrá dar por terminado el proceso. La variable Modif del algoritmo es la que detecta si se ha producido esta modificación de costes.
Es obvio que el número de veces que se ejecuta el bucle es como máximo |V|-1 y que, por lo tanto, la complejidad máxima es (|V|-1)|V|. En la práctica, el que se llegue o no a este máximo depende principalmente de lo similar que sea el orden en que se evalúan los vértices con respecto al orden "natural" del grafo (definido como la mejor aproximación posible a un orden topológico). Como ejemplo, se proporciona en la figura 5.4 un grafo que requiere el máximo número de reestimaciones, aunque no tiene circuitos, lo cual se ha conseguido simplemente evaluando en sentido inverso al "natural" los estados del grafo. El autor postula, pero no demuestra, que el número de reestimaciones es igual, como máximo, al número de aristas del grafo que sean contrarias al orden de evaluación (mas una). Un ejemplo de ello se muestra en la parte inferior de la misma figura.
La aplicación del algoritmo MINCIRCUITOS a un etapa de un trellis asociado a un autómata con circuitos es directa. De hecho, el algoritmo podría aplicarse a TODO el trellis en su conjunto (al fin y al cabo todo él es un grafo con circuitos), pero ello no se hace por la misma razón que no se hace en el algoritmo de Viterbi: se desaprovecharía la estructura multietapa del grafo.
Para una etapa del trellis, todos los vértices son iniciales (a todos llegan aristas de la etapa anterior) y todos son finales (de todos salen aristas a la etapa siguiente). Como los bucles son un caso particular de circuito, no es necesario considerarlos explícitamente en el que bautizaremos algoritmo CILICO (algoritmo para el análisis sintáctico corrector de erorres en autómatas con circuitos). Damos a continuación la versión iterativa del mismo, poniéndonos en el caso de gramáticas estocásticas, en el que el algoritmo CILICO es una extensión del ViterbiCorrector. Nótese que el algoritmo maximiza un producto lo cual no es problema, en contra de lo que pueda parecer después de lo dicho en el apartado anterior, puesto que todas las probabilidades son, por definición, menores que la unidad, con lo que su producto siempre decrece:
Algoritmo CICLICO /* A=(V,Q,qo,F,d) */
Datos /* [tau] es el tipo "estado", [sigma] el "símbolo", [psi] es el tipo "error */
V:C[sigma] Q:C[tau] qo:[tau] F:C[tau] a=a1a2...an:L[sigma]
resultado R:R
Auxiliar p:[tau]x[sigma]x[tau]->R /* probabilidad de una transición */
pe:[tau]x[psi]x[tau]->R /* probabilidad de error en una transición */
Variables P,P':C[tau]xR /* Vectores, indexados [tau] */
Modif:C[tau] /* Estados modificados */
HayModif:B /* Hay Estados modificados */
q,q':[tau] antes:R
Método
Aq'[propersubset]Q hacer P'[q']:=0 finA; P'[qo]:=1;
para j:=1..|a| hacer
Modif:=[emptyset]
Aq[propersubset]Q hacer /* Etapa del trellis: Primera evaluación */
P[q]:=max {
/* reglas de no error: q->aq', a=aj */
{P'[q'].p(q',aj,q)},
/* reglas de sustitución: q->ajq', a!=aj */
{P'[q'].p(q',sa|a,q)}
/* regla de inserción: q->ajq */
{P'[q].p(q,i,q)},
/* reglas de borrado: q->q' */
{P[q'].p(q',ba,q)}
}
Modif:=Modif+{q}
finA
Repetir /* Maximización de la etapa con circuitos */
HayModif:=falso
Aq[propersubset]Q hacer
antes:=P[q]
P[q]:=max {
/* reglas de borrado: q->q' */
{P[q'].p(q',ba,q)} }
si P[q]!=antes entonces HayModif:=verdad
finA
hasta no HayModif
P':=P
finpara
R:=
fin CICLICO
Se comprueba inmediatamente que las diferencias con el algoritmo ViterbiCorrector se centran exclusivamente en el tratamiento de los errores de borrado y en la supresión de la función "sig", ahora imposible. En la primera evaluación, se hace necesario restringir la maximización a los vértices ya calculados, especialmente al tratar con las aristas (transiciones) de borrado, únicas problemáticas; es para ello para lo que se usa el conjunto Modif. En la maximización de la etapa con circuitos se vuelven a comprobar estas mismas aristas de borrado, pero sólo éstas, puesto que son las únicas que pueden variar el resultado; el resto del algoritmo es idéntico a MINCIRCUITOS.
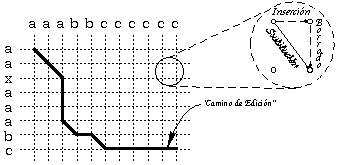
La derivación óptima, obtenida tras el análisis sintáctico corrector de errores de una cadena por una gramática (regular), está constituída por una secuencia de reglas, que el caso más general serán algunas pertenecientes a la gramática característica (reglas de no error), y otras a la expandida (reglas de error). Cada una de estas reglas ha sido utilizada para derivar un símbolo concreto de la cadena analizada, y está asociada (a través de la misma derivación óptima) a alguna de las reglas que se utilizarían para generar la cadena de la gramática más semejante (según el criterio de disimilitud utilizado, ver capítulo 2) a dicha cadena analizada. Toda esta información, directamente presente en la derivación óptima, se puede resumir de forma gráfica, habiéndose utilizado en este trabajo mayormente dos tipos de dibujo: la traza y el camino de edición.
Ambas representaciones gráficas son inmediatamente obtenibles, al igual que la derivación óptima, si durante análisis sintáctico por PD (p.e.: mediante ViterbiCorrector) se ha tomado la precaución de anotarse la decisión (transición) tomada en cada vértice del trellis. Una vez terminado el análisis, tanto la derivación óptima, como la traza y el camino de edición se extraen con sólo seguir las transiciones anotadas, empezando desde el último vértice del trellis (correspondiente al estado final y al último símbolo de la cadena), y terminando en el primero (correspondiente al estado inicial y al primer carácter de la cadena).
La traza de edición (ver figura 5.5) permite comparar la cadena de la gramática más semejante a la analizada con esta misma, mostrando qué símbolos de la cadena analizada han sido generados con reglas existentes en la gramática y cuáles por reglas de error. Se escriben las dos cadenas paralelamente la una a la otra, y se dibujan trazos continuos uniendo los símbolos que han sido generados por las mismas reglas (de no error). A veces también se unen, con trazos discontinuos, los símbolos generados por reglas de error, con los símbolos (de la cadena más semejante) generados por las reglas de la gramática característica asociadas a dichas reglas de error. Alternativamente a esto último, se pueden señalar con un subrayado los símbolos borrados o insertados (pero no los substituídos) [Sankoff,83].
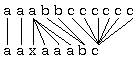
[1] Un estado q1 es predecesor de otro q si de q1 salen transiciones que llegan a q, es decir [existential]a[propersubset]V | d(q1,a)=q.
[2] De hecho, un grafo dirigido SIN circuitos es la representación usual para un orden parcial.
[3] Nótese que estas probabilidades NO son las probabilidades de deformación, son las probabilidades de las reglas, posiblemente relacionadas según indica el capítulo 2.
[4] El autor no puede dejar de señalar, sin pretensión alguna de demostralo, que su programa ERRPAR, que implementa la solución presentada más adelante, ya funcionaba antes de que el problema fuera abordado por estos otros autores.
[5] Esta rejilla y el camino de derivación equivalen (casi) al trellis que se tendría si el lenguaje de la gramática estuviera compuesto únicamente por la cadena más semejante a la analizada, y se marcara en él las reglas de la derivación óptima.