Los problemas de análisis sintáctico, en gramáticas regulares no deterministas (en las cuales se centra este capítulo), implican generalmente una búsqueda no trivial en el espacio de todas las posibles derivaciones. Esto es aún más inevitable en tanto en cuanto, en la mayoría de los casos prácticos, es imposible transformar una gramática no determinista en su correspondiente determinista, dado el enorme coste espacial (número de no-terminales o estados) que usualmente ello implica. El problema es especialmente agudo en reconocimiento sintáctico de formas, pues normalmente es necesario emplear gramáticas correctoras de errores, las cuales son innatamente no deterministas, y/o gramáticas estocásticas, en las cuales el análisis sintáctico consiste de por sí en el análisis de todas las posibles derivaciones (puesto que, en general, todas las reglas tienen alguna probabilidad de ser usadas). Las técnicas utilizadas en la práctica para llevar a cabo esta búsqueda en el espacio de derivaciones, se agrupan dentro del conjunto de algoritmos y técnicas de optimización conocido como Programación Dinámica (PD).
Las técnicas de programación dinámica resultan aplicables dado que el problema de análisis sintáctico en gramáticas regulares cumple el principio de optimalidad de Bellman. Una vez comprobado esto, el problema es sencillamente resoluble, con complejidad polinómica si se utilizan las verisones iterativas de los algoritmos, sólo con plantear el análisis sintáctico como la búsqueda de un camino óptimo en un grafo multi-etapa (conocido como <<celosía>> o <<retículo>>, o más usualmente por su nombre inglés: trellis).
En este contexto, "optimizar" equivale a seleccionar (buscar) la <<mejor>> solución de entre muchas posibles alternativas. Este proceso de optimización puede ser visto como una secuencia de decisiones que nos proporcionan la solución correcta. Si, dada una subsecuencia de decisiones, siempre se conoce cual es la decisión que debe tomarse a continuación para obtener la secuencia óptima, el problema es elemental y se resuelve trivialmente tomando una decisión detrás de otra, lo que se conoce como estrategia voraz.
A menudo, aunque no sea posible aplicar la estrategia voraz, se cumple el principio de optimalidad de Bellman [Bellman,57]: <<dada una secuencia óptima de decisiones, toda subsecuencia de ella es, a su vez, óptima>>. En este caso sigue siendo posible el ir tomando decisiones elementales, en la confianza de que la combinación de ellas seguirá siendo óptima, pero será entonces necesario explorar muchas secuencias de decisiones para dar con la correcta, siendo aquí donde interviene la programación dinámica.
Contemplar un problema como una secuencia de decisiones equivale a dividirlo en subproblemas de talla inferior, en principio más fácilmente resolubles. Ello se enmarca en el método de Divide y Vencerás [Horowitz,78], técnica similar a la de Programación Dinámica. La programación dinámica se aplica cuando la subdivisión de un problema conduce a:
* Una enorme cantidad de subproblemas.
* Subproblemas cuyas soluciones parciales se solapan.
* Grupos de subproblemas de muy distinta complejidad.
circunstancias que en conjunto o por separado, llevarían a una complejidad exponencial de la estrategia "Divide y Vencerás".
La versión recursiva del método de programación dinámica se resume en el siguiene esquema:
Esquema PDR(D:d):[rho]
Auxiliar contorno:d->B inicializa:d->[rho] [circlemultiply]:[rho]x[rho]->[rho]
elemental:dxd->[rho] decide:C[rho]->[rho]
descompone:d->Cdxd
Método
si contorno(D) entonces devuelve inicializa(D)
sino
devuelve {PDR(Z)[circlemultiply]elemental(Z,z)}
finsi
fin PDR
La idea del método consiste en subdividir el problema D en un conjunto de pares de subproblemas, uno trivial (resuelto mediante "elemental") y otro de complejidad <<menor>> que D, que a su vez se subdivide en pares de subproblemas y así sucesivamente. La recursión prosigue hasta alcanzar el problema de talla mínima (detectado por "contorno") cuya solución devuelve "inicializa". En cada paso, "decide" escoge, de entre todas las subdivisiones del problema proporcionadas por "descompone", aquella que nos lleva a la solución <<óptima>>. [circlemultiply] va combinando las soluciones elementales, proporcionando el resultado cuando se deshace la recursión.
Dos puntos deben resaltarse en este esquema:
* Puede ocurrir que se tenga que resolver varias veces el mismo
subproblema, al presentarse éste en varias ramas distintas de la
recursión, lo que en el caso general nos llevará a una
complejidad exponencial.
* La solución obtenida es <<óptima>> sólo
en el sentido indicado por "decide", cambiando esta función se
pueden obtener resultados completamente distintos, cada uno óptimo a su
manera.
Con el fin de reducir la complejidad de exponencial a polinómica, evitando recalcular subproblemas ya calculados, se transforma este esquema recursivo en uno iterativo:
Esquema PDI(D:d):[rho]
Auxiliar contorno:d->B inicializa:d->[rho] [circlemultiply]:[rho]x[rho]->[rho]
elemental:dxd->[rho]
decide:C[rho]->[rho]
descompone:d->Cdxd siguiente:d->d
do:d /*Primer subproblema (según siguiente) no en contorno*/
Variables d:d
G:Cdx[rho] /*Almacén de resultados intermedios, indexado por d*/
Método
Ad[propersubset]d si contorno(d)
entonces G[d]:=inicializa(d)
finA
si ~contorno(D) entonces
d:=do
bucle
G[d]:={G[Z][circlemultiply]elemental(Z,z)}
si d=D entonces salirbucle finsi
d:=siguiente(d)
finbucle
finsi
devuelve G[D]
fin PDI
La función "siguiente" ordena el espacio de subproblemas de tal manera que todo problema <<menor>> que uno dado se resuelve antes. Los problemas que no tienen subproblemas <<menores>> se resuelven al principio mediante "inicializa"; a partir de ellos los demás problemas se calculan siguiendo el orden definido y almacenando los resultados intermedios en G. De esta manera, cuando en cada punto se deba resolver un conjunto de subproblemas para que "decide" pueda escoger entre ellos, todos los subproblemas menores ya habrán sido resueltos y sus resultados se hallarán disponibles en G. La solución a cada subproblema se obtiene entonces evaluando un subproblema elemental y combinándolo mediante [circlemultiply] con un resultado contenido en G.
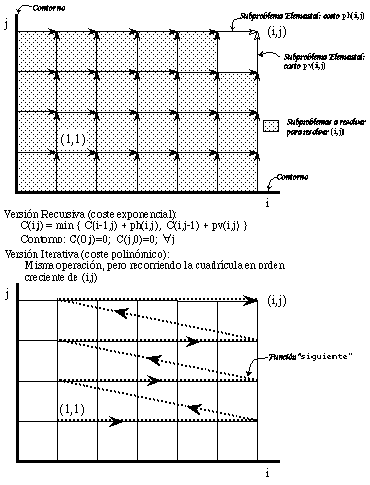
En la figura 4.1 se muestra la resolución por PD (en su versión iterativa y recursiva) del problema de encontrar el camino de coste mínimo entre dos vértices de un grafo dirigido y ponderado en forma de cuadrícula.
Asumiendo costes unitarios para las operaciones elementales, la complejidad temporal de la versión iterativa de programación dinámica es O(k.m), donde k es el máximo número de subproblemas en los que se puede subdividir un subproblema y m es el número de subproblemas "diferentes" del problema a resolver:

El análisis sintáctico en gramáticas regulares no deterministas se basa en un problema típicamente resoluble mediante programación dinámica: la búsqueda del camino de coste mínimo (o máximo) en un grafo multietapa.
Se define un grafo dirigido G=(V,A) como un conjunto V devértices (también llamados nodos) y un conjunto A={(u,v): u[propersubset]V, v[propersubset]V} de arcos. Si el grafo es ponderado, habrá además un peso (definido en el conjunto [rho]) asociado a cada arco: p:A->[rho]. Un grafo multietapa es un grafo en el que (figura 4.2):
* El conjunto de vértices está particionado en K
etapas:
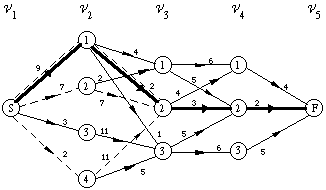
Se considera el problema de encontrar un camino que, yendo desde un vértice inicial a uno final de un grafo multietapa ponderado, extremice el coste acumulado C según cierto operador [circlemultiply] (suma de pesos, producto de pesos, operación booleana...). Para este problema es posible obtener inmediatamente la relación de recurrencia que lo resuelve por programación dinámica:
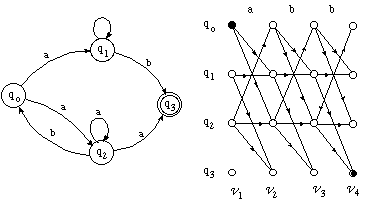
Para todo par (autómata finito, cadena de terminales), es posible asociarle un grafo multietapa ponderado, conocido con el nombre de trellis (palabra inglesa para "celosía"), de tal manera que el problema del análisis sintáctico de la cadena por el autómata se transforma en la búsqueda de un camino mínimo en dicho grafo.
Dado el autómata A=(V,Q,d,qo,F) y la cadena a=a1,a2,...,an, el trellis asociado T(V,A) se define de la siguiente manera (figura 4.3):
* Cada etapa tiene tantos vértices como estados del autómata;
hay una etapa por símbolo de la cadena, más una inicial:
* El conjunto de vértices finales está constituído por
aquellos vértices de la última etapa que corresponden a estados
finales del autómata: F={(n,q):q[propersubset]F}.
* Los pesos están definidos en el dominio de los booleanos, siendo
"verdad" el peso del arco ((j-1,w),(j,u)) si el estado u pertenece a
los sucesores de w cuando aparece el símbolo aj de la
cadena:
El algoritmo de Viterbi fue inicialmente desarrollado para encontrar, dada una secuencia de símbolos, la serie de transiciones más probable entre los estados de una cadena de Markov necesaria para producir dicha secuencia [Forney,73]. Este problema es el equivalente markoviano al análisis sintáctico en una gramática regular estocástica.
El algoritmo de Viterbi es un caso particular del algoritmo de Programación Dinámica utilizado para encontrar un camino extremal en un grafo multietapa. Al igual que en el caso del análisis sintáctico para gramáticas regulares no deterministas, se recurre a un trellis, pero en este caso se define la función peso, no el dominio de los booleanos, sino en el intervalo [0..1], puesto que ahora representa la probabilidad de una regla o transición:
La versión iterativa del algoritmo de Viterbi se deriva inmediatamente de la transformación recursivo-iterativa expuesta para el esquema general de Programación Dinámica. El coste temporal del algoritmo es del mismo orden que el utilizado en el caso del análisis sintáctico en autómatas no estocásticos (y no deterministas): O(n.|Q|.B). En cuanto al coste espacial, en principio de O(n.|Q|), se puede reducir a O(|Q|) teniendo en cuenta que en cada etapa sólo se requieren los valores de costo de la etapa anterior. Se puede entonces almacenar sólo éstos últimos olvidando los de las etapas precedentes, ya utilizados; con lo que solo es necesario emplear dos vectores que se desplazan por el trellis (llamados aquí P y P'), en vez de la matriz G completa:
Algoritmo VITERBI
Datos /* [tau] es el tipo "estado", [sigma] el "símbolo", A=(V,Q,qo,F,d) */
V:C[sigma] Q:C[tau] qo:[tau] F:C[tau] a=a1a2...an:L[sigma]
resultado R:R
Auxiliar p:[tau]x[sigma]x[tau]->R /* probabilidad de una transición */
Variables P,P':C[tau]xR /* Vectores, indexados por t */
q,q':[tau]
Método
Aq'[propersubset]Q hacer P'[q']:=0 finA
P'[qo]:=1;
para j:=1..|a| hacer
Aq[propersubset]Q hacer P[q]:={P'[q'].p(q',aj,q)}
finA
P':=P
finpara
R:=
fin VITERBI
El algoritmo, tal como se describe más arriba, sólo nos proporciona el coste final (probabilidad) de la derivación más probable. Para conocer la derivación misma es necesario apuntarse, en cada paso de la recursión, qué decisión se ha tomado, con el fin de poder luego conocer la secuencia de reglas (estados) que se han utilizado. Ello incrementa la complejidad espacial otra vez en una cantidad equivalente al numero de vértices del trellis, con lo que nos queda otra vez O(n.|Q|)
En aplicaciones prácticas es posible reducir drásticamente (en algunos casos hasta 1/30) el coste temporal mediante la aplicación simultánea de varias técnicas diferentes como pueden ser:
* Considerar para la decisión en cada etapa únicamente los
estados alcanzados.
* Búsqueda en Haz (<<Beam Search>>), en la que
sólo se consideran los "mejores" caminos explorados, desechando los
demás.
Un estudio detallado de éstos y otros métodos se halla en [Torró,89].