La utilización en la práctica de los métodos sintácticos de reconocimiento de formas viene condicionada, no sólo por la necesidad de tener resuelta la etapa de representación, que en la suposición de que los objetos se presten a una descripción en términos de subobjetos, se resume en disponer de un método satisfactorio de selección y/o extracción de los mismos, sino también por la obligatoriedad de conocer la descripcción estructural de todos los posibles objetos que toman parte de la forma. Es decir, es necesario conocer la gramática. Como generalmente ello no es posible a priori, se hace necesario construirla u obtenerla mediante algún método de aprendizaje; y dado que en la mayoría de los problemas de reconocimiento de formas la única información de que se dispone (o se es capaz de transmitir) sobre la forma se halla resumida en un conjunto de ejemplos, se recurre usualmente a métodos de aprendizaje inductivo, que en el caso de los métodos sintácticos se engloban en lo que se conoce como inferencia gramatical (IG) [Fu,75] [Miclet,90].
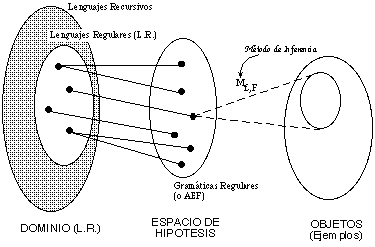
Al igual que cualquier otro problema de inferencia Inductiva, la inferencia gramatical se especifica mediante la definición de [García,88]:
a) Un dominio de formas a inferir.
b) Un espacio de hipótesis o representaciones.
c) Un método de presentación de ejemplos.
d) Un método de inferencia.
e) Un criterio de éxito.
Usualmente las aplicaciones prácticas descartan, por su intratabilidad, la utilización de los métodos enumerativos de inferencia gramatical, centrándose en métodos constructivos, los cuales utilizan normalmente sólo muestras positivas. La gran mayoría de los métodos de inferencia gramatical existentes en la actualidad son métodosheurísticos (no caracterizables) e infieren gramáticas regulares.
Para la inferencia gramatical el dominio de formas es cualquier subconjunto de los lenguajes formales. Más concretamente, se le restringe a cualquier subconjunto de los lenguajes recursivos. (los lenguajes recursivos son aquellos lenguajes formales LcV* sobre el alfabeto V, para los cuales es decidible si una cadena a[propersubset]V* pertenece o no a dicho lenguaje).
El espacio de las hipótesis depende del dominio de formas que debe de inferir el sistema y de la representación utilizada. Como única condición, debe de estar compuesto de por lo menos una representación (descripción de una hipótesis) para cada forma (en nuestro caso, lenguaje) del dominio. En particular, en el caso de que se trate de inferir un lenguaje de la subclase de los lenguajes regulares sobre un alfabeto V, el espacio de las hipótesis lo forman las gramáticas regulares sobre V, aunque también lo podrían serlo los autómatas finitos sobre V.
En general en inferencia inductiva se utilizan dos métodos de presentación de ejemplos [Gold,67]:
* Presentación positiva del lenguaje L: es una
sucesión de elementos de L (muestras positivas).
* Presentación completa del lenguaje L: es una
sucesión de elementos de L y de su complementario (muestras positivas y
muestras negativas), marcados para indicar su pertenencia o no a L.
Todas las cadenas de V* aparecen en la secuencia.
Ambos métodos son utilizados en inferencia gramatical, aunque básicamente se emplee la presentación positiva por las razones que se expondrán más adelante.
Que consiste en un algoritmo que a cada nuevo ejemplo proporciona una forma (su representación, la hipótesis) válida (o no) para los ejemplos presentados hasta ese momento. Expresado formalmente, un método de inferencia M[sterling],[Gamma] es una función M[sterling],[Gamma]:2[Theta]->H, donde 2[Theta] es el conjunto de todos los subconjuntos finitos del espacio de objetos [Theta] (de cadenas de V* para la IG), [sterling] el dominio y H el espacio de las hipótesis. [Gamma] es el criterio de preferencia que utiliza el método para escoger la siguiente hipótesis Ht[propersubset]H, válida para el conjunto de ejemplos {a1,...,at}, cuando le llega el ejemplo at en el instante t (ver figura 3.1).

Existen dos tipos básicos de métodos de inferencia, los:
* Constructivos, que van construyendo una nueva hipótesis con
cada nuevo ejemplo.
* Enumerativos, que asumen que es posible enumerar las
hipótesis. A cada nuevo ejemplo, un método enumerativo
buscará secuencial y exahustivamente en la lista de hipótesis la
primera que sea compatible con todos los ejemplos presentados.
En inferencia gramatical, como en casi todos los casos prácticos de reconocimiento de formas, se emplean métodos constructivos que usualmente son conservativos y consistentes.
Si un proceso de inferencia se considera infinito, se puede determinar su éxito estudiando su comportamiento en el límite. El criterio de éxito más fuerte que se puede exigir es que el método dé con la solución correcta, es decir, que a partir de cierto momento (de cierto ejemplo) no cambie de hipótesis y que la hipótesis que tiene en ese momento sea la buena (lo que no quiere decir que el método sepa detenerse en ese punto). Este es el criterio de identificación en el límite.:
Se dice que un conjunto de lenguajes recursivos es identificable a partir de presentación completa si para cualquier lenguaje L del conjunto y cualquier secuencia infinita de cadenas de L, existe un algoritmo que identifica a L en el límite.
Un método de inferencia es más potente que otro, si dado un criterio de éxito y un método de presentación, el conjunto de lenguajes que es capaz de inferir (su alcance) es más amplio. Puesto que los métodos enumerativos se basan en una búsqueda exahustiva del espacio de las hipótesis, es evidente que pueden inferir cualquier clase de lenguajes, y que por lo tanto son de una potencia insuperable. Toda limitación en la potencia de los métodos enumerativos será pues válida también a los otros métodos de inferencia, lo que permite limitar el estudio teórico a los enumerativos, más sencillos conceptualmente.
El tiempo de convergencia de un método de inferencia se define como el punto (número del ejemplo) a partir del cual se se ha conseguido la identificación en el límite. Un método es uniformemente más rápido que otro cuando, sea cual sea la presentación, su tiempo de convergencia es menor en por lo menos uno de los lenguajes a inferir (y no es mayor para ningún otro de estos lenguajes). Un teorema de Gold [Gold,67], establece que, para un determinado lenguaje y una determinada presentación, no existe un algoritmo uniformemente más rápido que el correspondiente método enumerativo.
Desgraciadamente, es muy difícil implementar en la práctica un método enumerativo: la complejidad de la búsqueda exahustiva que implican crece exponencialmente con la talla del espacio de las hipótesis. A pesar de ello, algunas variantes de los métodos enumerativos han sido estudiadas. Estos algoritmos, que se basan en estructurar el espacio de las hipótesis con alguna relación más compleja que la simple enumeración, consiguen disminuir drásticamente la complejidad de la búsqueda en algunos casos concretos (Poda, Búsqueda en un retículo,...) [García,88].
Dos teoremas básicos, también debidos a Gold, delimitan drásticamente lo que posible aprender mediante cualquier método de inferencia [Gold,67]:
* Cualquier clase de lenguajes recursivos primitivos es
identificable en el límite a partir de presentación completa.
* Si una clase de lenguajes recursivos contiene todos los
lenguajes finitos y al menos uno infinito (se dice que es superfinita),
entonces no es identificable mediante presentación positiva.
Estos teoremas no hacen más que asentar formalmente un razonamiento intuitivo elemental: si no se dispone de muestras negativas es imposible limitar la generalización efectuada por el método de inferencia: cualquier hipótesis cuyo lenguaje sea un superconjunto del buscado será compatible con los datos. Con todo, un corolario inmediato evidencia que la clase de los lenguajes regulares no es identificable en el límite a partir de presentación positiva.
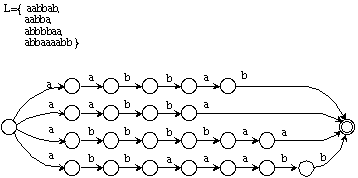
A pesar de lo anterior, la mayoría de los sistemas de inferencia gramatical sólo utilizan muestras positivas, principalmente debido a que los métodos enumerativos no son lo suficientemente rápidos, y los métodos constructivos existentes no permiten la utilización de muestras negativas. Otra razón, de no menos peso en la práctica, reside en el hecho de que, prescindiendo de consideraciones teóricas, no es necesario identificar perfectamente un lenguaje para poder construir un sistema reconocedor que funcione. En un clasificador, por ejemplo, basta con que el lenguaje inferido contenga al de una clase y no se intersecte con los de las otras clases. Por otra parte, no es necesario empeñarse en inferir lenguajes superfinitos: existen clases de lenguajes identificables en el límite a partir de presentación positiva. Por ejemplo, cuando los lenguajes de una clase son todos finitos, ésta es identificable con sólo ir construyendo el autómata canónico (si el lenguaje es finito, es regular) (figura 3,2).
Generalmente, en un proceso de inferencia a partir de ejemplos la solución no es única, debiéndose en la práctica escoger, de entre un conjunto de soluciones posibles, la solución que mejor se adapte a la aplicación en particular. Esta elección presupone la introducción en el proceso de inferencia de un conocimiento adicional, que se puede aportar de dos maneras, correspondientes a dos clases de métodos de inferencia [Angluin,83] [Garcia,90]:
* Métodos heurísticos, en los que el conocimiento
está incluído en el heurístico que define el procedimiento
de generación de la siguiente hipótesis. Lo ideal es que se
emplee un heurístico lo más ceñido posible al campo de
aplicación, para así evitar hipótesis inconsistentes con
dicho campo. En este tipo de métodos no suele ser posible definir
formalmente el dominio de lenguajes que infieren.
* Métodos caracterizables, en los que la hipótesis
siguiente se escoge siempre dentro de una clase de lenguajes conocida y bien
definida (que generalmente formará parte de los "inferibles mediante
presentación positiva" según el teorema de Angluin). Aquí,
el conocimiento del problema se introduce escogiendo la clase de lenguajes
cuyas propiedades sean apropiadas para la aplicación concreta.
En la práctica, y dada la escasez existente de métodos caracterizables cuyos lenguajes sean utilizables en aplicaciones reales, los diseñadores acaban escogiendo algún método heurístico conocido, procediendo a adaptarlo a su problema concreto. A esto se añade la dificultad de que la mayoría de los métodos heurísticos disponibles actualmente se han diseñado de manera de aprovechar ciertas propiedades generales de los lenguajes regulares (lema de la estrella, equivalencia de los buenos finales,...), con lo que resultan poco aplicables en la práctica.
Por otro lado, recientemente se ha propuesto una nueva metodología que permite desarrollar nuevos métodos de inferencia gramatical, en los que el conocimiento a priori se incorpora con cierta facilidad en base a las propiedades requeridas para el lenguaje buscado [García,88].
Por razones como las expuestas en apartados anteriores, la gran mayoría, por no decir todos, los métodos prácticos de inferencia gramatical son constructivos y utilizan únicamente presentación positiva. A su vez, de entre todos ellos, la gran mayoría está orientada a la inferencia de lenguajes regulares, siendo escasos los que infieren gramáticas de contexto libre o superiores [García,88].
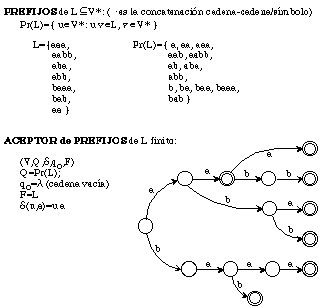
De entre los métodos de inferencia de gramáticas regulares (autómatas) caben destacar los que se basan en distintos métodos de agrupar los estados del autómata árbol aceptor de prefijos (ver figura 3.3) de las muestras positivas. Este autómata proporciona un espacio de búsqueda muy adecuado, siempre que la muestra sea estructuralmente completa (se ha utilizado para generarla todas las reglas de la gramática a inferir).
Ejemplos de este tipo serían (ver [García,88] para una breve explicación de cada uno): método de las k-colas, que se basa en la "equivalencia de los buenos finales" [Biermann,72]; algoritmo k-RI, que infiere lenguajes regulares de la subclase de los "k-reversibles" [Angluin,82]; inferencia de lenguajes k-contextuales [Muggleton,84], que produce resultados similares al anterior; y otros dos también basados en los "buenos finales": método de Levine [Levine,82] y método de comparación de finales [Miclet,80].
Finalmente, métodos como el presentado en este trabajo (ECGI) y otros expuestos en el capítulo 7 [Chirathamjaree,80] [Thomason,86] [Falaschi,90], utilizan la corrección de errores para construir incrementalmente gramáticas, añadiendo a cada nueva muestra únicamente las reglas necesarias para que sea aceptada.