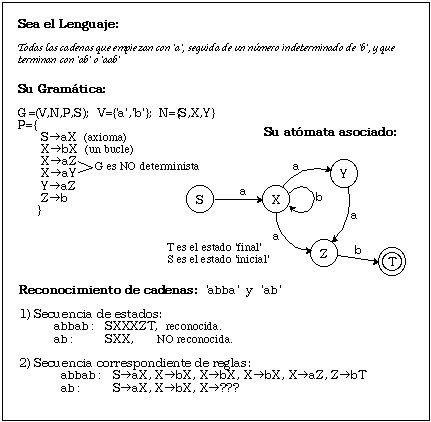
Entre los métodos estructurales de reconocimiento de formas destacan los métodos englobados en lo que se conoce como reconocimiento sintáctico de formas. Estos métodos intentan aprovechar las técnicas desarrolladas por la teoría de lenguajes formales [Aho,73] [Eilemberg,74] [Harrison,78], las cuales proveen de una representación (las gramáticas) y de un mecanismo de interpretación ("parsing" o análisis sintáctico) para aquellas formas cuyos objetos se pueden describir como cadenas de subobjetos [Gonzalez,78] [Fu,82] [Miclet,86].
En su utilización en reconocimiento de formas, la teoría de lenguajes tropezó desde un principio con un problema inherente a este dominio de aplicación: la representación imprecisa de los objetos. Para solventar esta dificultad se hace necesario recurrir a métodos de análisis sintáctico tolerantes a cadenas "ruidosas" o plagadas de errores. Los más desarrollados de estos métodos son el análisis sintáctico corrector de errores y el análisis sintáctico estocástico, que utilizados simultáneamente permiten construir analizadores sintácticos correctores de errores estocásticos.
Dado un conjunto de símbolos o alfabeto V, el conjunto de todas cadenas posibles sobre ese alfabeto es V* (el monoide libre sobre V mediante el operador concatenación) y V+ será el mismo conjunto sin la cadena vacía. Un lenguaje sobre el alfabeto V es un subconjunto de V*. Existen un número no enumerable de lenguajes, todos ellos representables mediante gramáticas.
Una gramática se define como la cuádrupla G=(N,V,P,S), donde V es el alfabeto de G y N es un conjunto finito de símbolos no terminales, V[intersection]N=Ø. Se conoce a W=VuN como el vocabulario de G, una frase [zeta][propersubset]W* es una cadena de símbolos de W. PcW*NW*xW* es un conjunto de reglas de producción o reescritura, que transforman una frase (en la que por lo menos hay un no terminal) en otra frase del mismo vocabulario. Estas reglas se denotan como [zeta]1A[zeta]2->[zeta]3, donde [zeta]1,[zeta]2,[zeta]3[propersubset]W* y A[propersubset][Nu]. Finalmente, S[propersubset]N es el símbolo no terminal inicial o axioma de G.
Mediante la aplicación sucesiva de reglas de G se puede transformar una frase [zeta]1 del vocabulario en otra [zeta]n. Escribiremos esto como [zeta]1[zeta]n; [zeta]1,[zeta]n[propersubset]W*; y si D([zeta]n)=([zeta]1,[zeta]2,[zeta]3,...,[zeta]n), [zeta]i[propersubset]W*, es la secuencia de frases que han llevado de [zeta]1 a [zeta]n, diremos que D es una derivación de [zeta]n desde [zeta]1. Se define entonces el lenguaje generado por G como el conjunto de todas las cadenas del alfabeto que se pueden derivar del axioma de G: L(G)={ a : a[propersubset]V*, Sa }.
Al proceso de obtener una derivación de una cadena a partir del axioma de una gramática y aplicando reglas de ésta, se le denomina análisis sintáctico. Se dice que una gramática es ambigua si para alguna cadena del lenguaje existe más de una posible derivación para generarla.
Chomsky dividió las gramáticas (y por lo tanto los lenguajes) en una jerarquía que va del tipo 0 a 3, en orden decreciente de complejidad, y en base a la forma de sus reglas:
Tipo 0: Gramáticas sin restricciones en las reglas.
Tipo 1: Gramáticas sensibles al contexto, con reglas de la forma [zeta]1A[zeta]2->[zeta]1[beta][zeta]2. Es decir, el no terminal A se sustituye por la frase [beta] del vocabulario en el contexto [zeta]1[zeta]2 ([zeta]1,[zeta]2[propersubset]W*, [beta][propersubset]W+).
Tipo 2: Gramáticas de independientes del contexto, en las que A->[beta] independientemente del contexto.
Tipo 3: Gramáticas regulares, cuyas reglas son de la forma A->aB o A->a; a[propersubset]V; A,B[propersubset]N.
La gramáticas de tipo 0 y 1 son las que proporcionan el mayor poder descriptivo, aunque son las gramáticas del tipo 2 y 3 las más utilizadas en aplicaciones prácticas como el reconocimiento de formas, principalmente debido a su mucho menor complejidad. Todas ellas son las llamadas gramáticas formales.
Según se ha definido en el apartado anterior, para cada lenguaje existe una gramática generadora del mismo. Similarmente, existe un reconocedor capaz de decidir si una cadena pertenece o no a dicho lenguaje.
Para los lenguajes regulares el reconocedor es un autómata finito. Se demuestra que para todo autómata finito existe una gramática regular que genera el lenguaje aceptado por el autómata y viceversa [Aho,73].
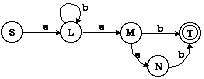
Un autómata finito se define como una quíntupla A=(V,Q,d,qo,F), donde V es un conjunto finito de símbolos y Q un conjunto finito de estados. qo es el estado inicial y FcQ el conjunto de estados finales. d una función de transición entre estados: d:(QxV)->P(Q). El funcionamiento de un autómata se inicia en qo para ir pasando, mediante la función de transición, de un estado al estado siguiente según indiquen los sucesivos símbolos de la cadena a reconocer. Si después del último símbolo de la cadena se ha llegado a un estado final, la cadena pertenece al lenguaje del autómata (figura 2.1). Formalmente, el lenguaje de cadenas de V* aceptado por el autómata A se define como L(A)={a|a[propersubset]V* [logicaland] [Delta](qo,a)hF!=Ø}, donde [Delta]:(QxV*)->P(Q) es la función de transición d extendida a cadenas de símbolos ([lambda] es la cadena vacía):

La definición de los reconocedores de lenguajes conduce inmediatamente a una posible manera de utilizar los métodos sintácticos en reconocimiento de formas. Para ello, y siempre que los objetos sean representables mediante cadenas de símbolos, basta construir un clasificador en el que se define una gramática por clase o forma. El correspondiente reconocedor (p.e., un autómata si la gramática es regular) determinará si la cadena pertenece o no al lenguaje de la gramática (al conjunto de cadenas que éste representa) y por lo tanto, a la forma. La construcción o inferencia de los reconocedores asociados a cada clase, o equivalentemente de sus gramáticas, se puede llevar a cabo manualmente o mediante métodos de inferencia gramatical (ver capítulo siguiente).
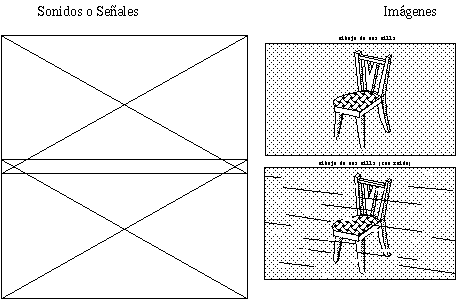
Es muy usual en reconocimiento de formas el que los objetos a reconocer, e incluso los ejemplos de aprendizaje, vengan distorsionados y embrollados por ruidos de diversa procedencia (medio ambiente, líneas de transmisión en mal estado, mancha en la foto,...) (figura 2.3).
* Aquellas en las que la interpretación se lleva a cabo mediante el
uso de métodos derivados de la teoría de la decisión,
definiendo una distancia entre cadenas, a partir de información
estadística relativa a los distintos errores debidos al ruido u otras
causas [Aho,72] [Aho,73] [Thomason,74] [Bahl,75] [Tanaka,86] [Tanala,87]. Las
técnicas correspondientes se engloban en el llamado análisis
sintáctico corrector de errores.
* Aquellas que asocian a la información estructural una
información probabilística, sobre la frecuencia de
uso/aparición de las distintas partes de la estructura. Este suplemento
de información flexibiliza notablemente la capacidad de
representación del modelo, y ha conducido a la extensión de los
lenguajes formales con el fin de incluir en ellos los llamados lenguajes
estocásticos. Estos lenguajes se representan mediante
gramáticas estocásticas, con las que se lleva a cabo un
análisis sintáctico estocástico [Gonzalez,78]
[Fu,82].
La idea básica del análisis sintáctico corrector de errores reside en la estimación de una distancia o medida de similitud entre una cadena distorsionada y su original perteneciente a una gramática dada.
La distancia entre dos cadenas se define a partir del "número mínimo" de transformaciones de error necesarias para pasar de una cadena a la otra. Se consideran tres tipos posibles de error: borrado, inserción o sustitución de un símbolo, pudiéndose pasar de una cadena a otra cualquiera simplemente mediante combinación de estos errores [Thomason,74] [Fu,82]. Formalmente, se definen tres transformaciones:
borrado: aa[beta] a[beta];
inserción: a[beta] aa[beta];
sustitución: aa[beta] ab[beta]
Tb,Ti,Ts : V*->V*; a,[beta][propersubset]V*; a,b[propersubset]V; a!=b;
a partir de las cuales se define la distancia de Levenshtein dL(a,[beta]) entre dos cadenas a,[beta][propersubset]V* como el mínimo número de transformaciones necesarias para convertir a en [beta] (figura 2.4). Es decir, si C es cualquier secuencia de transformaciones que convierta a en [beta] y SC, BC, IC son respectivamente el número de sustituciones, borrados e inserciones en C:

Una vez definida la distancia, un algoritmo analizador sintáctico corrector de errores es un algoritmo que busca una cadena [beta] perteneciente al lenguaje de la gramática G tal que la distancia (d) entre [beta] y la cadena a analizar a sea mínima:
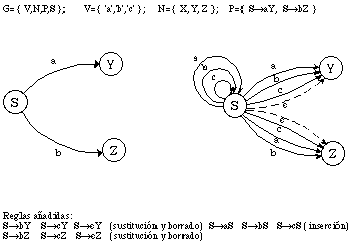
* Construcción de la gramática expandida
Ge de la gramática G original, añadiendo a cada regla
de G sus correspondientes reglas de error. Existirá una regla de
error asociada a cada posible transformación de error (figura 2.5).
Concretamente, las reglas de error a añadir a una gramática regular G=(N,V,P,S) para construir su gramática expandida serán, Ax[propersubset]V, ([epsilon] es el símbolo nulo nil):
Inserción (de x): A->xA A(A->bB)[propersubset]P
Sustitución (de b por x): A->xB A(A->bB)[propersubset]P; A->x A(A->b)[propersubset]P
Borrado (de b)[1]: A->B A(A->bB)[propersubset]P; A->[epsilon] A(A->b)[propersubset]P
Típicamente, los algoritmos que se emplean para esta búsqueda y minimización son los mismos que los utilizados para gramáticas no deterministas, por lo que se basan también en las técnicas de programación dinámica. Sin embargo, la particular forma de las reglas de borrado obliga a utilizar algoritmos especiales, algunos de los cuales se proponen en el capítulo 5.
Una gramática estocástica se forma añadiendo probabilidades a las reglas de una gramática no estocástica (la gramática característica de la gramática estocástica). El lenguaje estocástico generado por tal gramática está formado no sólo por las cadenas del lenguaje, sino también por su probabilidad de producción, que se obtiene mediante el producto de las probabilidades de las reglas utilizadas.
La teoría de las gramáticas estocásticas está perfectamente asentada, con una teoría matemática que complementa a la de los lenguajes formales. Por ejemplo, una gramática estocástica regular es equivalente (o se puede modelizar como) un generador de Markov [Casacuberta,90b], el cual destaca por ser uno de los procesos estocásticos más tratables y mejor comprendidos [Rabiner,89a].
Una gramática ponderada es una quintupla Gs=(N,V,P,S,D). Donde G=(N,V,P,S) es la gramática característica de la gramática ponderada y D es el conjunto de pesos asociado a las reglas de P. Para cada regla [zeta]1iAi[zeta]2i->[zeta]ij el peso se escribe pij (i=1,...,K; j=1,...,ni; K es el número de partes izquierdas distintas y ni el número de reglas con la parte izquierda i). Se dice que Gs es estocástica si los pesos se comportan como probabilidades, es decir, si pij[subset]]0,1] y la suma de las probabilidades de todas las reglas con la misma parte izquierda es igual a la unidad:
Una gramática estocástica es no-restringida si la probabilidad de una regla no depende de la secuencia de reglas anteriormente aplicada. En una gramática no-restringida (y no ambigua), la probabilidad de generación de una cadena a=a1a2...am; a1,a2,...,am[propersubset]V, a partir del axioma S, aplicando la secuencia de reglas r1,r2,r3,...,rm, viene dada por p(a)=p(r1).p(r2).....p(rm), donde p(ri) es la probabilidad de la regla ri. Escribiremos esto Sa.
En una gramática ambigua, existirán na secuencias de reglas (derivaciones) para generar la misma cadena a, cada una con su respectiva probabilidad pi(a), i=1,...,na. En este caso la probabilidad de generación de a se puede definir de dos posibles maneras:
* suma de la probabilidad de un número finito de eventos excluyentes
(aproximación aditiva):
Del mismo modo en que se extienden las gramáticas para obtener gramáticas estocásticas, se pueden extender los reconocedores para obtener reconocedores estocásticos. En concreto, para las gramáticas estocásticas de tipo 3 o regulares, los reconocedores designados serán los autómatas finitos estocásticos, que se derivan de los autómatas finitos añadiendo probabilidades a las transiciones.
Un autómata finito estocástico (AFE) es una quíntupla As(Q,V,d,I,F), donde Q es un conjunto finito de estados y V el conjunto de símbolos terminales. d:QxExQ->0,1] es una función parcial que asigna las probabilidades a todas las posibles transiciones. I:Q->[0,1], F:Q->{0,1} definen para cada estado su probabilidad de ser inicial y su pertenecia o no al conjunto de estados finales, respectivamente. Para asegurar la estocasticidad, la suma de probabilidades de las transiciones que salen de un mismo estado debe ser igual a la unidad:
Si el AFE es no-restringido (la probabilidad de una transición es independiente de las de las demás transiciones) la probabilidad de aceptar una cadena a=a1a2...an siguiendo la secuencia de estados qo,q1,...,qn se escribe como:
Dada una gramática estocástica regular, existe un AFE que acepta un lenguaje idéntico al generado por la gramática (pero lo contrario no es cierto) [González,78] (figura 2.6).
En el aprendizaje de gramáticas estocásticas, no sólo se debe de tener en cuenta la estructura de los ejemplos, sino también la frecuencia de aparición de los mismos. Para ello, el método generalmente empleado se basa en la adquisición independiente del modelo estructural (de la gramática no estocástica), añadiéndose con posterioridad las probabilidades de las reglas mediante un análisis estadístico de los ejemplos y de sus derivaciones por la gramática [Maryanski,77] [Chandhuri,86]. Más raramente, es el propio proceso de inferencia de las reglas (estructura) el que se ve guiado por el comportamiento estadístico de los ejemplos [Thomason,86].
Consideraremos aquí únicamente el proceso de inferir las probabilidades de las reglas de una gramática característica G=(V,N,P,S) ya conocida. Dicho de otro modo, se trata de inferir el conjunto de probabilidades D de la gramática estocástica Gs correspondiente a G, a partir de un conjunto de m ejemplos X={a1,...,am} con frecuencias respectivas de aparición f1,...,fm. Entonces, y siempre que G no sea ambigüa, la probabilidad por máxima verosimilitud pij de la regla [zeta]1iAi[zeta]2i->[zeta]ij se puede estimar en base a:
Obsérvese que el procedimiento de estimación descrito no es válido en el caso de gramáticas ambiguas, pues no se ha definido ningún método para "distribuir" las probabilidades cuando hay más de una derivación. En el caso concreto de las gramáticas estocásticas ambigüas regulares existen métodos adecuados, entre los que cabe destacar, por su uso generalizado, el algoritmo de <<Baum-Welch>> y el de reestimación por Viterbi [Levinson,83] [Rabiner,89].
A la hora de efectuar el análisis sintáctico de cadenas muestras deformadas, es posible combinar en un solo proceso las dos estrategias presentadas en los apartados anteriores, obteniéndose entonces la metodología conocida como elanálisis sintáctico corrector de errores estocástico. La idea de este método consiste simplemente en aplicar a las gramáticas estocásticas el mismo procedimiento de corrección de errores que se utilizó para las gramáticas no estocásticas; para lo cual, a una gramática estocástica se le añadirá el modelo de corrección de errores (las reglas de error) [Thomason,75]. Como la gramática expandida resultante deberá ser estocástica también, es necesario complementar cada transformación de error, no sólo con un peso como en la distancia de Levenshtein y la de Fu, sino con una probabilidad. En estas condiciones, la similitud entre cadenas no se mide mediante una distancia entre ellas, sino por la probabilidad de que una se transforme en otra. El análisis sintáctico corrector de errores no minimizará una distancia, sino que maximizará una probabilidad.
Utilizando un modelo de error similar[3] al utilizado como ejemplo en el apartado 2.4.1, las transformaciones de error posibles serán: inserción de un símbolo 'b' (antes de otro 'a', a,b[propersubset]V), borrado del mismo (substitución de a por [epsilon], el símbolo nil), y sustitución de 'a' por otro símbolo 'b'. A cada uno de estos errores se le asocia una probabilidad, respectivamente pi(a|b), pb([epsilon]|a) y ps(b|a). Denotaremos ps(a|a) a la probabilidad de sustituir 'a' por sí mismo, es decir, la probabilidad de que NO se produzca error en 'a' (probabilidad de no error). Nos referiremos a una cualquiera de estasprobabilidades de deformación, como pd. A partir de estas definiciones, y por extensión, pueden definirse la probabilidad de transformar un símbolo en una cadena y, aún con más generalidad, la de una cadena a en otra cadena [beta]: p([beta]|a) [Fu,82].
Un analizador sintáctico corrector de errores estocástico buscará la cadena [beta] del lenguaje de la gramática G que maximize a la vez la probabilidad de que la cadena a (que no pertenece a dicho lenguaje) se pueda transformar en [beta] y la probabilidad de que [beta] sea del lenguaje:
La probabilidad que maximiza la expresión anterior:
En los restantes capítulos de este trabajo se tratará exclusivamente con gramáticas regulares (y en su mayoría estocásticas). En particular, en las implementaciones prácticas se ha recurrido a una subclase de las gramáticas de tipo 3: las gramáticas SANSAT ("SAme Non-terminal, then SAme Terminal"), de las cuales el autor no ha encontrado en la literatura ninguna mención explícita. Una gramática G=(N,V,P,S) será una SANSAT, si cumple la condición de que todas las reglas que tienen el mismo no terminal a la derecha tienen también el mismo terminal:
Dada una gramática regular G=(N,V,P,S), una gramática SANSAT equivalente a ella, Gt=(Nt,V,Pt,S), se construye de la siguiente manera (ver figura 2.7):
* Se genera un no terminal por cada parte derecha de regla diferente:
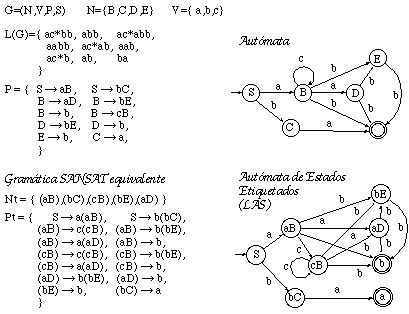
Un autómata de estados etiquetados LAS=(Vt,Q,d,qo,F,E), es un autómata equivalente a una gramática SANSAT G=(Nt,V,Pt,S), construído de manera similar a la seguida usualmente para obtener el autómata equivalente a una gramática, pero:
* Se añade una función de etiquetado E:Q->V que asigna a
cada estado el símbolo terminal asociado a todas las reglas con ese no
terminal a la derecha. Por completitud de E, se etiqueta arbitrariamente el
estado inicial con el símbolo "~", (símbolo inicial) que se
añade al conjunto de terminales.
* Se obliga a que haya tantos estados finales como símbolos
terminales puedan terminar una cadena del lenguaje.
Todo lo cual queda expresado formalmente como sigue:
Vt=V u {~}; ~[reflexsubset]V
Q={ qaA: A XaA[propersubset]Nt } u F; F={ qa : A a[propersubset]V, (XbA->a)[propersubset]Pt }; qo=S;
d:QxV->Q;
d={ (qaA, b, qbB) : si (XaA->bXbB)[propersubset]Pt } u { (qo, a, qaA) : si (S->aA)[propersubset]P };
E:Q->V; E(qo)=~; E(qaB)=a; E(qa)=a;
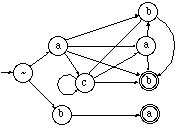
En un LAS, los terminales asociados a las transiciones son siempre iguales a la etiqueta el estado destino de la transición. Esto permitiría definir las transiciones sin etiquetas (terminales asociados), al ser éstas redundantes, pero se las ha conservado para permitir que un LAS siga siendo un autómata en el sentido clásico. Por otra parte, gracias a esta propiedad, un LAS puede ser representado esquemáticamente de idéntica manera que un autómata clásico, pero etiquetando los estados en lugar de las transiciones (ver figura 2.8). También aprovechando esta propiedad es posible dar una definición alternativa del lenguaje del LAS: una cadena es reconocida por un LAS (y por lo tanto pertenece a su lenguaje) si existe un camino en el LAS que partiendo del estado inicial llegue a uno final, tal que la secuencia de etiquetas de estados se corresponda con la secuencia de símbolos de la cadena:
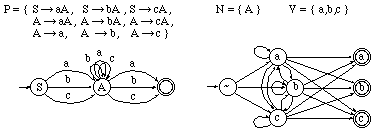
Es extremadamente interesante notar cómo, a partir de la equivalencia entre una gramática regular y un autómata de símbolos etiquetados, es inmediato relacionar las gramáticas con losModelos Ocultos de Markov (Hidden Markov Model: HMM [Rabiner,89a]) con estados finales. En efecto, si se define un autómata estocástico de estados etiquetados, como un LAS, con:
* Probabilidades de transición p(q|q') (la probabilidad de una
transición no depende del símbolo).
* Una función de etiquetado E(q,a):QxV->[0..1]
probabilística (probabilidad de que la etiqueta de q[propersubset]Q sea
a[propersubset]V).
de forma que:
[1] Según la definición más corriente, estas reglas NO SON REGULARES. Esto se discute con detalle en el Capítulo 5.
[2] La derivación óptima puede no ser única.
[3] En este caso, el coste de inserción depende del símbolo antes del cual se realiza la inserción.
[4] Basta notar que, en realidad, lo que se está haciendo es desdoblar los no terminales (estados) en tantos como sea necesario para que a cada uno de ellos llegue siempre el mismo terminal.