La idea de utilizar un método de corrección de errores como punto de partida para la inferencia de modelos estructurales no es exclusiva de ECGI. Se resumen a continuación los trabajos de cuatro autores en este campo (únicos conocidos por el autor).
En el mismo congreso en que ECGI se presentó por primera vez [Rulot,87] M.G.Thomason expuso, también por primera vez, un algoritmo basado en una idea similar a ECGI, pero destinado específicamente a la inferencia de redes de Markov, método que fué publicado unos meses más tarde [Thomason,86] [Thomason,87]. Posteriormente [Gregor,88] adaptó el método añadiendo la posibilidad de imponer ciertas restricciones (puntos de identificación forzosos) al proceso de inferencia.
El modelo inferido es parecido al ECGI. No tiene circuitos, son los estados los que llevan los símbolos y sólo existe un estado final. Las redes son igualmente no deterministas y ambiguas [Gregor,88]. Por otro lado, al ser un modelo Markoviano, es estocástico desde un principio y tiene asociadas probabilidades a las transiciones y los estados.
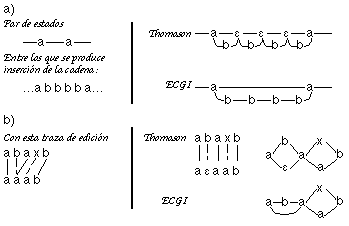
Sin embargo, a diferencia del ECGI, se autorizan estados etiquetados con el símbolo nil, y los modelos son mucho más lineales. Ello es debido a que en construcción sólo se aplican criterios locales: se añaden directamente las reglas de error (ver figura 12.1).

En la comparación se utiliza una distancia probabilística basada en las probabilidades de las transiciones y de los nodos (frecuencia relativa de uso de los mismos hasta ese momento por R+). Las probabilidades de las transiciones de error se definen con coste fijo (se aplica el mismo modelo de deformación que en ECGI) (ver figura 12.2).
El modelo de error es el mismo en reconocimiento, no pareciendo preocuparse en ningún momento los autores de la estocasticidad de la gramática expandida. Sí que se preocupan de renormalizar en cada paso las probabilidades, manteniendo en todo momento la estocasticidad de la gramática que se infiere y que aprovechan durante la inferencia. Ello, desde luego implica un coste superior al ECGI, pues obliga a una normalización y cálculo de logaritmo por cada transición de la gramática expandida; esto en reconocimiento es obviable, pues la normalización puede hacerse de una vez por todas.
En cuanto a los resultados obtenidos, el método se ha utilizado en la inferencia de muestras sintéticas [Thomason,87], cromosomas [Gregor,88] y palabra hablada [Thomason,86].
En el modelo de Thomason, si fij es la frecuencia de utilización (hasta ese momento, por R+) del arco desde el nodo si al sj, entonces la probabilidad de una transición es:
d(i,j)=max {
/* Borrado */ d(i,j-1) .
/* Substitución */ d(i-1,j-1) ..
/* Inserción */ d(i-1,j) ..
}
Recientemente A.Falaschi ha presentado un nuevo método, en el que utiliza ideas de construcción y simplificación de autómatas muy relacionadas con las utilizadas por ECGI [Falaschi,90] [Falaschi,90a], al que referencia explícitamente como un método similar.
Al igual que para el método de Thomason, el objetivo del método de Falaschi es la inferencia de redes de Markov. El método también está basado en la programación dinámica, la cual utiliza en tres de los 5 pasos de que consta el método:
1) Ordenar las cadenas de R+. La ordenación se basa en la probabilidad de las cadenas (obtenida a partir de la frecuencia de los símbolos que las componen) y en su desviación respecto a la longitud media.
2) Alineamiento de todas las cadenas mediante programación dinámica a una longitud fija e igual a la de la cadena mejor según la ordenación. La alineación se optimiza respecto a todas las cadenas anteriores, que se ponen en paralelo en uno de los ejes del trellis. La distancia escoge en cada punto el símbolo más parecido (al de la nueva muestra) que se encuentra en ese sitio en cualquiera de ellas, con la restricción añadida de que intenta evitar borrados de símbolos muy frecuentes e inserción de símbolos cerca de los extremos de la cadena.
3) "Colapso" del autómata canónico así obtenido, uniendo todos los estados con el mismo símbolo en la misma posición y almacenando la frecuencia de uso de cada nuevo estado y transición.
4) Generación, a partir del autómata colapsado, de una secuencia de muestras "más probables", también mediante programación dinámica y aplicando una distancia basada en la frecuencia de uso de los estados y transiciones. Después de cada optimización, que proporciona una nueva cadena óptima para la red en ese paso, se suprime la transición menos probable antes de realizar el siguiente alineamiento.
5) Construcción, a partir de las muestras generadas del autómata, mediante el siguiente algoritmo [Falaschi,90]:
Algoritmo Falaschi-Construcción
Datos Sk[propersubset]V*, k=1..Ns /* muestras generadas */
Método
Generar el grafo inicial a partir de So asignando a cada símbolo su correspondiente estado.
para k=1..Ns hacer
para h=1..k-1 hacer
Alinear Sk con Sh
si la distancia es mínima /* Ah */
entonces Dopt:=Dkh /* derivación de Sk con Sh */
fin para
Añadir los estados relacionados por Dopt que tengan distinto símbolo.
Generar las transiciones indicadas por Dopt entre estados presentes y presentes y/o añadidos.
fin para
fin Falaschi-Construcción
La distancia para el alineamiento se define en este último paso como:
D(n,m) = d(Sk(n),Sh(m)) + min { D(n-1,m-1),
D(n-1,m)+1, /*inserción*/
D(n,m-1)+1 /*borrado*/ }
con d(Sk(n),Sh(m))=2+[epsilon], [epsilon]>0 si Sk(n)!=Sh(m) y 0 si no (distancia entre el carácter n de la cadena k y el m de la cadena h).
Obviamente este último paso es el que más relacionado está con ECGI aunque utiliza una distancia, en absoluto equivalente, en la que los distintos errores tienen distinto coste (p.e: da ventaja a inserción seguida de borrado frente a sustitución, según Falaschi para forzar la inserción seguida de borrado si esto permite alinear dos símbolos iguales).
Falaschi no da aquí por terminado el proceso de aprendizaje, y reestima los parámetros del modelo de Markov inferido, al que añade un modelo duracional original [Falaschi,90b], utilizando procedimientos clásicos (Viterbi, Forward-Backward). El mismo modelo duracional es el que se emplea en reconocimiento, y es por lo tanto totalmente distinto al usado en construcción y al empleado por ECGI.
Con todo lo dicho, se hace muy difícil una comparación de resultados, aunque el mismo Falaschi admite que los suyos son pobres: 70% (pero se trata de una tarea de reconocimiento de fonemas).
El proceso de generación de muestras "sintéticas" recurre a un método de simplificación progresiva de una red, muy parecido al que utiliza ECGI para simplificar autómatas (ver capítulo 10). El criterio para encontrar la transición que debe borrarse recurre a la búsqueda del segundo camino mínimo, en el que se aplica un heurístico poco fiable (que el segundo camino no empieza y termina en los mismos estados que el primero [Falaschi,90a]). Curiosamente Falaschi no intenta usar el autómata "colapsado" directamente en reconocimiento (aunque sea simplificándolo).
Las estructuras inferidas deben de ser muy parecidas a las construídas por ECGI (Falaschi no introduce el símbolo nil en sus modelos), y si el método de generar muestras sintéticas funciona, tendrían que ser menos complejas (a menos de utilizar ECGI con reducción de estados), debiéndose obtenerse resultados comparables. Nótese que el ECGI con reducción de estados se ha utilizado para la misma tarea de inferir redes de Markov [Casacuberta,90], que luego son reestimadas mediante Baum-Welch. La diferencia principal con el método de Falaschi reside en que éste reduce la información antes de la construcción.
Por su interés y relación bastante directa con las ideas de ECGI, es necesario mencionar el trabajo de Chirathamjaree y Ackroyd [Chirathamjaree,80], en el que se presenta un interesante método incremental para la inferencia de gramáticas independientes del contexto.
Las gramáticas que infiere este método quedan restringidas a reglas de la forma:
A->aB; A->Ba; A->a;
(gramatica lineal a izquierda y derecha); también están libres de circuitos y en ellas todas las cadenas generables a partir de un no terminal dado son de la misma longitud (siendo el axioma una excepción).
El método, que se inicializa generando la gramática canónica trivial para la primera cadena, aprovecha las peculiaridades impuestas a la gramática y rellena, a cada nueva muestra y mediante un algoritmo de programación dinámica, una matriz mijk en la que cada elemento contiene el coste mínimo de generar, a partir del no terminal k-ésimo de la gramática, la subcadena de longitud i, que empieza en el símbolo j-ésimo de la muestra.
Basándose en esta matriz, se aplica todo un conjunto de reglas para añadir a la gramática el mínimo número de no terminales y reglas necesarios para generar la nueva muestra, induciéndose, como en el caso de ECGI, una generalización.
El método puede evidentemente utilizarse para generar gramáticas regulares. El coste de evaluación de la matriz cúbica no es mencionado (sólo es necesario calcular la mitad de ella) y, desgraciadamente, los autores no proporcionan ningún resultado de aplicación a un caso real. Todo ello hace imposible ninguna comparación sin la implementación efectiva del método.
En [Marco,88] se presenta una generalización de la idea de ECGI, aplicándola a gramáticas independientes del contexto. Se aplica el mismo modelo de error que ECGI para extender la gramática, aunque para el análisis sintáctico se hace necesario emplear el algoritmo de Eearley [Fu,82]. Un procedimiento que involucra un "traductor incorporado" permite evitar de construir el árbol de derivación a la hora de obtener la derivación óptima. Una vez obtenida esta última, se añaden a la gramática las reglas de error, con el fin de que esta última pueda reconocer a la cadena muestra. Los autores no llegan a realizar la extensión estocástica y no presentan resultados en aplicaciones prácticas.
En reconocimiento del habla se han utilizado muy a menudo, y con muy buenos resultados dos métodos muy diferentes, y con los que es conveniente comparar ECGI: los modelos ocultos de Markov y el alineamiento temporal no lineal.
Para el reconocimiento sintáctico de cadenas de símbolos, es muy corriente la utilización de los modelos ocultos de Markov (Hidden Markov Models: HMM), siendo gracias a éstos con los que se han obtenidos algunas de los mejores tasas de aciertos en reconocimiento de formas. Ello es debido a su gran flexibilidad de definición estructural, a la existencia de muy eficaces y bien conocidos métodos de entrenamiento, a la capacidad intrínseca que poseen de tratar con el tiempo (longitud) y su facilidad de combinación para formar redes más complejas.
Es normal en reconocimiento de la palabra utilizar HMM muy reducidos (5 a 20 estados por palabra, a veces 30), constreñidos a estructuras lineales de izquierda a derecha y al sencillo modelo de error (transiciones permitidas) utilizado en este trabajo. Con estas limitaciones, se obtienen fácilmente tasas superiores al 90% en reconocimiento de dígitos [Rabiner,83].
Dicho esto, es inmediato preguntarse si las estructuras inferidas por el ECGI no son simplemente una versión compleja de los HMM, dada la equivalencia formal que existe entre los LAS estocásticos y los HMM.
Esto ha sido estudiado, y en [Casacuberta,90] se presenta los resultados mostrados en la tabla 12.1, obtenidos con el experimento HLKO (ver capítulo 8):
ECGI 99.8 642 196 (media)
HMM8 98.5 135 8
HMM8S 98.7 141 8
En la que se evidencia que para un mismo conjunto de datos ECGI obtiene una tasa de reconocimiento 1.9% mejor que un HMM estándar de 8 estados.
Para obtener con modelos de Markov una eficiencia similar a ECGI se postula que probablemete serían necesario disponer de más de 3 HMM por palabra, entrenados mediante técnicas adecuadas de clustering [Rabiner,89], o utilizar HMM mucho más largos, del orden de 30 estados. Esta última aproximación, llevada a cabo en [Casacuberta,91] efectivamente permite obtener los mismos resultados que ECGI (tabla 12.2, con el mismo experimento); e incluso a veces mejores con sólo 20 estados (tabla 12.3, experimento LLKO).
ECGI 99.8 642 196 (media)
HMM10 99.7 168 10
HMM30S 99.8 537 30
ECGI 73.8 2360 785 (media)
HMM10 67.6 338 10
HMM20 75.0 678 20
HMM20S 62.7 697 20
HMM30 73.7 1018 30
Otras alternativas, que también aumentan el coste espacio-temporal de los HMM hasta aproximarlos al ECGI involucrarían un mejor modelizado de la duración (p.e.: Probabilidades de transición continuas [Falaschi,90b]).
La mucho mayor complejidad temporal del ECGI, debida al gran número de estados, puede reducirse drásticamente utilizando las técnicas presentadas en [Torró,89] y [Torró,90] (Sólo estados alcanzados, Búsqueda en Haz, Reconocimiento Anticipado) consiguiéndose, con el mismo conjunto de datos, las mismas tasas de reconocimiento, visitando tan sólo un 9% de los estados (17 estados en este caso). La complejidad espacial del ECGI no es tan grande como parece, en relación con los HMM: el número de parámetros de los HMM de 30 estados es de 537, y para los autómatas de ECGI con 196 estados es 642. El incremento muy grande del número de parámetros que se observa para el ECGI, en el caso del experimento con EE-letras, es debido al mucho mayor número de símbolos, que no sólo aumenta mucho la variabilidad (y por lo tanto el número de estados de los modelos inferidos por ECGI), sino además multiplica el número de probabilidades de error (la talla de la tabla de sustitución crece con el cuadrado del número de símbolos). Téngase además en cuenta que, con las técnicas presentadas en el capítulo 10, es posible reducir drásticamente el número de estados de los modelos inferidos por ECGI. Una reducción que llegue al un número de estados eqivalente en los HMM -30- todavía consigue un 99% de aciertos, y ello, con un número de parámetros mucho menor y peor estimados que los HMM (puesto que la estimación de parámetros se ha hecho con el modelo sin reducir).
Una técnica aún más clásica que los HMM, y también relacionada de algún modo con el ECGI, consiste en utilizar el alineamiento temporal no lineal (DTW) [Casacuberta,87] de la cadena muestra con un conjunto de N patrones (utilizando la regla de decisión K-NN), generamente obtenidos mediante técnicas de clustering a partir de las muestras de R+.
Mediante DTW se consiguen porcentajes de reconocimiento iguales o superiores a los obtenidos mediante HMM, estando generalmente la diferencia justificada por la cantidad de datos disponibles (la gran cantidad de parámetros a estimar probabilísticamente siempre ha sido el talón de aquiles de los modelos estocásticos) y por la utilización de símbolos discretos o vectores de parámetros reales. En [Rabiner,83] se realiza un estudio comparativo muy detallado y exahustivo, donde se muestra que DTW (12 patrones/clase) llega a obtener hasta un 3% de ventaja sobre los HMM (5 estados) si se les entrena con 100 a 200 patrones (la tarea es otra vez el reconocimiento de dígitos ingleses hablados, cuantificando con 64 símbolos). Utilizando vectores en vez de símbolos se mejora el DTW en otro 3%, una mejora que probablemente se extendería a los HMM en el mismo caso.
La diferencia entre los dos modelos, es en el fondo la diferencia entre un modelo paramétrico (estructura fija, gran número de parámetros a estimar estadísticamente) y otro no paramétrico (estructura desconocida, comparación mediante distancia con patrones almacenados), y los resultados de [Rabiner,83] indican que se pueden considerar complementarios.
ECGI, de alguna manera es una forma compacta de almacenar todos las cadenas de R+ como patrones, postulando además una generalización sobre ellas. En reconocimiento ECGI lleva efectivamente a cabo DTW "en paralelo" para todos los patrones (y su generalización). Ahora bien, en el caso de los dígitos hablados, los trellis asociados a ECGI tienen un número menor de vértices que en el caso de DTW con sólo 5 patrones/clase (~130 vértices por símbolo de entrada, longitud media de las muestras: 30), obteniendo resultados equivalentes (mejores), aún en el caso de tener muy pocos símbolos discretos (~15); gracias precisamente a su poder de generalización.
De hecho, ECGI con símbolos discretos ha demostrado proporcionar resultados equivalentes o mejores que un DTW con vectores de parámetros y 18 a 20 patrones por clase, utilizando el mismo corpus de datos de dígitos hablados (aunque distribuídos de manera distinta) [Vidal,88b]. En el caso multilocutor, DTW obtuvo un 99% de aciertos, ECGI (experimento H2 capítulo 8) 100%; en el caso independiente del locutor DTW obtuvo 97% y ECGI un 98% a 100% (experimentos H1, H3, H4 y H5 y H6).
La complejidad temporal crece en ambos casos linealmente con el número de patrones/estados, y aunque es cierto que la complejidad de un DTW se puede reducir grandemente utilizando métodos eficientes de búsqueda de los vecinos más próximos [Vidal,88a], también es cierto, como se ha visto antes, que la complejidad de ECGI se puede reducir considerablemente.
Es posible considerar al ECGI como un modelo intermedio entre DTW y HMM, que pretende aprovechar las ventajas de uno y otro (utilizar todas las muestras como patrones de referencia, obtener directamente de ellas el modelo estructural y los valores de los parámetros).
Del mismo modo que DTW, mediante ECGI se podría obtener provecho de la utilización de vectores de parámetros en vez de símbolos discretos; de hecho actualmente ésta es una de las primeras mejoras que se prevee implementar (ver epílogo y apéndice A).
Los mismos experimentos de reconocimiento de formas realizados con dígitos manuscritos e impresos han sido realizados utilizando métodos de parametrización y reconocimiento más clásicos en reconocimiento de imágenes (manuscritos [Vidal,91] [Vidal,92a], impresos [Vidal,92] ).
Como parámetros se emplearon momentos geométricos [Teague,80] [The,88]: 7 momentos centrales normalizados del área del objeto (dígito) y 7 momentos centrales normalizados del contorno del mismo. Estos momentos aseguran una invarianza a la escala y a la traslación, pero no a la rotación ni a la reflexión. Estos dos últimos tipos de invarianza implicarían el recurso a momentos invariantes, los cuales resultan inadecuados en nuestro caso, pues algunos dígitos se pueden convertir en versiones muy similares de otros a través de una serie de reflexiones y giros [Vidal,91].
Los 14 parámetros así obtenidos forman un punto en un espacio 14-dimensional, el cual se clasifica siguiendo la regla de los k vecinos más próximos (k-NN) [Duda,73]), empleando como prototipos todas las muestras de aprendizaje (200 por clase para el caso de los dígitos manuscritos, 280 en el caso de los impresos, y un valor de k igual a 45 y 40 respectivamente).
Para poder tener en cuenta la diferente naturaleza de los grupos de componentes de los vectores, se escoge una distancia ponderada, concretamente, la distancia de Mahalanobis con matriz de covarianza diagonal:
Los experimentos realizados se corresponden con los experimentos de "leaving-k-out" de dígitos manuscritos e impresos. En el caso de los impresos, se realizaron eliminando el tipo Helvética del conjunto de datos. La tabla 12.4 evidencia la superioridad de ECGI para las tareas planteadas.
| Método
|
ECGI
Estocástico,
Sólo substituciones.
|
K-NN
| |||
| Resolución
(Pixels)
|
Rej4
|
Rej6
|
Rej8
|
Rej10
|
1
|
| Dígitos
manuscritos
|
|||||
| Tamaño
medio de los modelos
|
310
|
223
|
176
|
144
|
200
|
| %Aciertos
|
98,0
|
98,15
|
96,92
|
96,31
|
81,5
|
| Dígitos
impresos
|
|||||
| Tamaño
medio de los modelos
|
249
|
170
|
130
|
111
|
240
|
| %Aciertos
|
99,18
|
98,75
|
98,14
|
97,32
|
90,2
|
En el caso más general, y considerando el estado del arte expuesto en el capítulo 1 (98 a 99% en dígitos manuscritos aislados), se puede afirmar que el ECGI se sitúa entre los mejores métodos utilizados para el reconocimiento de dígitos, ello aún sin introducir refinamientos específicos a la tarea (parametrización más adecuada, invarianza a la rotación, etc...) que podrían aumentar notablemente la sus capacidades de reconocimiento.