Este capítulo se divide en dos partes bien diferenciadas. En la primera de ellas se realiza una modificación (subóptima y heurística) al método de construcción de ECGI con el fin de conseguir que éste genere gramáticas deterministas (y por lo tanto no ambiguas). En la segunda parte se propone un nuevo método, basado en autómatas inferidos por ECGI, para obtener la cadena mediana de un conjunto de cadenas.
La posible ambigüedad de las gramáticas generadas por ECGI imposibilita, no sólo la estimación correcta (mediante métodos de reducida complejidad) de las probabilidades de las reglas utilizadas en su extensión estocástica, sino también la estimación exacta del número de cadenas distintas del lenguaje de la gramática. Esta mayor complejidad de tratamiento, debida a la ambigüedad, se extenderá a muchos otros posibles tratamientos y análisis a los que se desee someter las gramáticas generadas por ECGI.
Una manera sencilla e inmediata de hacer desaparecer la ambigüedad consiste en forzar a ECGI a generar gramáticas deterministas. El determinismo de las gramáticas es además una propiedad interesante por sí misma (p.e.: si no se utiliza corrección de errores permite realizar el análisis sintáctico sin tener que recurrir a Viterbi).
En los siguientes apartados se introduce una modificación de la etapa de comparación de ECGI, que permite obligar a éste a generar gramáticas deterministas.
No es conveniente intentar introducir el determinismo en la etapa de construcción de ECGI. Ello supondría alterar la asignación de reglas efectuada por la optimización, sin ninguna garantía de mantener una mínima optimalidad. En efecto, si una nueva regla fuera imposible por ser no determinista, sería necesario volver a buscar por toda la gramática dónde y cómo intercalar óptimamente la subcadena que ha quedado desconectada, y ello desde luego, manteniendo la coherencia con los heurísticos de ECGI (ausencia de circuitos, de transiciones nil, etc...).
Es pues en la búsqueda de la derivación óptima donde se introduce el conocimiento de cómo opera la etapa de construcción, para así prevenir la generación de derivaciones que conduzcan a construcciones no deterministas.
Examinando la etapa de construcción de ECGI, se comprueba que toda nueva transición que es añadida a un estado existente, se corresponde con un punto de la derivación óptima donde, a continuación de una regla de no error, aparece una regla de error (es un punto donde la cadena se separa de la cadena más próxima de la gramática). Para asegurar el determinismo basta entonces rechazar, durante la búsqueda de la derivación óptima, toda derivación que demuestre tener una regla de no error seguida de una de error (A->bB)(B->cX); y ello, siempre que el símbolo asociado a la regla de error aparezca en una regla ya existente con el mismo no terminal a la izquierda, p.e.: (B->cC).
Formalmente, ello equivale a decir: si Gi=(Ni,V,Pi,S) es la gramática actual del paso i-ésimo de una inferencia por ECGI, y D(xi,Gi)=r1,r2,..,rs,rs+1,..,rk; rj[propersubset]Pei; j=1..k; rs=(A->bB)[propersubset]Pi; rs+1=(B->cX)[propersubset]Pei; es una derivación de xi[propersubset]V* en Gi extendida a errores Gei=(Ni,V,Pei,S), y m(B->cC)[propersubset]Pi; entonces D(xi,Gi) no es una derivación admisible para el método ECGI determinista.
Esta condición es imposible de imponer conservando la complejidad del algoritmo ViterbiCorrector, pues incumple el principio de optimalidad de Bellman: no se puede determinar si desde un principio se está escogiendo una derivación que en su mitad va a ser prohibida, por lo que no se puede garantizar que una decisión local sea óptima. El método propuesto asume esta no optimalidad para poder generar gramáticas deterministas, y por lo tanto, en el método ECGI determinista, el proceso de búsqueda de la derivación que minimiza la disimilitud es subóptimo (o el que maximiza la similitud).
En la práctica, pues, se mantiene el algoritmo ViterbiCorrector, sólo que en el proceso de optimización se rechaza, en un punto dado del trellis, aquella decisión que, en la posterior construcción, llevaría al no determinismo. Con esta condición, el cálculo de ViterbiCorrector deberá obligatoriamente progresar de atrás hacia delante, puesto que es necesario, para decidir si se acepta una regla como de no error, tener la regla siguiente (anterior en el cálculo) para comprobar si cumple la condición.
Aparece entonces otro problema, también debido a la no optimalidad del procedimiento empleado, y que reside en el principio de la cadena: cuando llega el momento de la última decisión, ésta puede ser imposible. En efecto, si la segunda regla es de error, la primera deberá cumplir la condición de determinismo. Esto puede forzar a descartar todas las derivaciones que partan sin error del axioma, si con todas ellas ocurre lo mismo (téngase en cuenta que la decisión es local, no se puede volver atrás). El siguiente es un ejemplo de esta situación (en negrita las reglas de error, ~ representa la axioma, e,d[propersubset]V; E,D[propersubset]N; ):
La solución adoptada no puede ser más pragmática: toda cadena cuya derivación "óptima" determinista empieze con una regla de error es descartada. Es decir, en la inferencia de gramáticas deterministas, ECGI descarta ciertas cadenas patrón por ser incompatibles con la gramática determinista que construye.
Se supone que estas cadenas son resultado de algún error poco usual, y que la información útil que transportan será aportada por otra cadena patrón más adelante. Ello en el caso general será cierto si el número de muestras de aprendizaje es suficiente. En el peor de los casos habrá que aumentar ligeramente este número pues, tal como se comprueba de forma empírica, suelen descartarse menos de un 20% de cadenas. Alternativamente sería posible, una vez consideradas todas las muestras, reconsiderar aquellas que han sido descartadas, en la esperanza (bastante plausible, al haber crecido notablemente la gramática) de que esta vez serán aceptadas.
Obsérvese que, aunque la gramática así obtenida es determinista, ello no implica que su inversa lo sea. Al invertir las transiciones puede perfectamente ocurrir que un estado sea origen de más de una transición con el mismo simbolo. Lo que sí es invariable a una inversión es la ambigüedad: tanto la gramática como su inversa serán no ambiguas; si no hay ningún camino igual a otro en uno de los sentidos, tampoco lo habrá en el contrario.
Por otra parte, la aplicación de un algoritmo determinista imposibilita prácticamente, si se opta por un proceso de aprendizaje continuo, la integración inferencia-reconocimiento del algoritmo de optimización, a menos se se tolere la intrínseca suboptimalidad de este último durante el reconocimiento.
Como se mencionó cuando se explicó el algoritmo de construcción para un LAS (autómata de estados etiquetados: ver capítulos 2 y 6), el método ECGI determinista emplea un método de construcción ligeramente distinto a método estándar. Ello es debido a la necesidad que tiene de conocer puntualmente, en un punto dado del trellis, si la regla es o no de error.
En la implementación aquí realizada, y como ya se mencionó en el capítulo 6, ECGI representa los autómatas a la inversa, y que hace el barrido del trellis de adelante hacia atrás. Ello no modifica en absoluto las ideas expuestas en el apartado anterior: únicamente implica invertir las definiciones y explicaciones. Es decir, y resumidamente: en vez de buscar dónde se separan la muestra y la cadena más próxima se buscará donde se juntan. La condición de determinismo implica un par (X->aA)(A->bB) de regla de error seguida de no error (al contrario de lo antes definido), y la regla de error no debe tener el mismo símbolo que cualquier posible regla ya existente (C->aA). El problema de bordes aparecerá al final de la cadena.
Nótese que la inversión es debida al sentido del barrido, no de la representación. Aunque se calcule con las transiciones hacia delante, hay que usar esta última definición. Sin embargo, la inversión implica que el autómata obtenido es determinista deatrás hacia delante, es decir, el autómata que es determinista es el autómata inverso al obtenido.
Se describe a continuación el algoritmo que permite asegurarse, en el caso de un LAS, si la derivación es o no determinista en cada punto del trellis. El algoritmo se aplica en el momento de analizar una arista de substitución (pa,p):
Algoritmo Substitución Determinista
Auxiliar /* Las 2 primeras son funciones sobre un vértice del trellis */
q:QxV->Q /* estado asociado */
v:QxV->V /* terminal asociado */
eti:Q->V /* etiqueta de un estado (LAS) */
Datos
p[propersubset]QxV /* vértice examinado en el trellis */
pa[propersubset]QxV /* vértice del trellis anterior según */
/* la regla de susbtitución examinada */
Método
si v(p)=eti(q(p)) /* puede ser regla de no error */
y m qx:eti(q(pa))=eti(qx) y d-1(qx,eti(q((p)),q(p))
/* existe ya una transición con */
/* igual terminal */
entonces
si q(pa)=qx /* es la que se esta examinando */
y v(pa)=eti(q((pa)) y
TipoRegla(pt,pa)=Substitución
/* la regla anterior no es de error*/
entonces devolver coste (pa,p)
/* esta regla es de no error */
sino prohibir (pa,p)
/* es regla no determinista */
sino devolver coste (pa,p)
/* es regla de error o regla de no */
/* error aún no existente */
fin Substitución Determinista
Obsérvese que las condiciones de regla de no error son idénticas a las ya explicadas en el algoritmo ECGI-LAS (costrucción), para el caso no determinista, y que una de estas condiciones se aplica a una arista que parece indefinida (pt,pa). En la práctica esta arista es la que obliga el sentido de recorrido y está apuntada en la matriz de producciones (matriz que cada punto del trellis indica la arista de donde viene el camino óptimo hasta ese punto).
La que sí queda explícita es la condición de que, si la regla que se está examinando existe ya (es de no error), y la regla anterior es de error, se prohíbe la que se está examinando.
La aplicación de este algoritmo implica el coste añadido, sólo en el caso de aristas de sustitución, de 1 a 4 comparaciones, más un barrido de los predecesores del estado asociado al punto del trellis examinado, para comprobar si tienen el símbolo en cuestión.
La comprobación del efecto de borde se hace justo en el momento de iniciar la etapa de construcción, descartando la cadena si la última regla de la derivación es una inserción o un borrado (debido a la definición de LAS, si es una substitución, no es error; no se puede substituir el símbolo final).
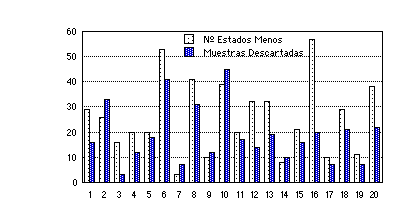
Para comprobar la efectividad del método de obtención de gramáticas deterministas, y para asegurarse de que el determinismo no implica pérdida de capacidad de reconocimiento (máxime teniendo en cuenta que se descartan cadenas de aprendizaje), se repitieron con la versión determinista de ECGI casi todos los experimentos de reconocimiento realizados con dígitos hablados (ver detalles en capítulo 8) (tabla 11.1). Al final de la inferencia de cada autómata, el método ECGI determinista comprueba (mediante el algoritmo trivial) que efectivamente el (inverso del) autómata generado es determinista.
El método ECGI determinista utiliza la maximización de aciertos como criterio de disimilitud durante la inferencia. Todos los experimentos mostrados se han realizado con el modelo de error completo en reconocimiento. Piloto NE se refiere a un experimento con el corpus piloto en el que no se utiliza la extensión estocástica.
Piloto 99,5 1063 98 1059 9%
Piloto NE 97,5 1063 99 1059 9%
H1 99,2 1533 99,2 1379 12,4%
HLKO11 98,2 1965 98,2 1699 17,6%
Ninguno de los autómatas inferidos durante los experimentos cuyos resultados se muetran en la tabla 11.1 ha resultado ser no determinista, lo que confirma el buen comportamiento del algoritmo propuesto. Lo más notable que se aprecia en la tabla es la nula pérdida (o ganancia) de capacidad de reconocimiento en (casi) todos los experimentos, a pesar de que (como se comprobó examinando uno por uno los listados de inferencia de los 50 autómatas de HLKO11) se descartaron en algunos casos hasta el 56% de las muestras de aprendizaje (este porcentaje resultó ser muy variable: del 1.3% a 56%). Los peores resultados de la versión determinista en el experimento básico en el el caso estocástico, se compensan con los mejores resultados para el caso no estocástico.
En cuanto al tamaño de los autómatas, se reduce de aproximadamente un 11% (en realidad un 8%, si se considera que el factor de ramificación aumenta ligeramente: 1.97 a 2.06 en HLKO11), pero es fácil comprobar que en gran parte es debido al menor número de muestras que se han utilizado en su inferencia (ver figura 11.1). Posiblemente las muestras descartadas son muestras con muchas pequeñas diferencias, compensadas en reconocimiento por el modelo de error. La estructura de los autómatas inferidos por la versión determinista es bastante similar a los inferidos por la versión no determinista (figura 11.2).

Dada una gramática (autómata) inferida por ECGI, la intuición sugiere que debe de ser posible encontrar una derivación o camino medio estructural que de alguna manera refleje la secuencia de reglas (estados o transiciones) o cadena más próxima (en el sentido de la corrección de errores) a todas las demás cadenas del lenguaje de la gramática (autómata). Esta es la que llamaremos cadena mediana de la gramática (autómata).
Si C={a1,a2,...,an} es un conjunto de n números reales, entonces, la media aritmética de C, que se escribe m, satisface la relación:
Alternativamente, si en vez de una medida de disimilitud, existe una función p:S->[0,1], =1, que proporciona la probabilidad de que xi[propersubset]S, el elemento más probable Mp:
Si la distribución en S es normal, Mp será también la media y la mediana de S, y Mg será a la vez la moda y la media.
Utilizando las definiciones del apartado anterior, [Kohonen,85] propone un método para obtener la cadena mediana de un conjunto de cadenas. El método de Kohonen es relativamente costoso, pues supone el buscar primero la mediana del conjunto (por el procedimiento más directo: calculando la matriz de distancias entre todas las cadenas del conjunto) y luego realizar variaciones sistemáticas (errores) sobre ésta hasta dar con la mediana.
Por otro lado, si la inferencia realizada por ECGI es adecuada, se espera que la cadena mediana del conjunto R+ esté muy próxima a la cadena más probable de la gramática inferida por ECGI (se está suponiendo que R+ tiene una distribución aproximadamente "normal" en el espacio V*).
La posibilidad de obtener la cadena mediana de R+ a partir del autómata generado por ECGI proporciona no sólo un nuevo método para obtener la cadena mediana (útil para extraer la cadena real a partir de un conjunto de muestras extremadamente ruidosas, ver ejemplos más adelante), sino que confirma que el autómata generado por ECGI modeliza adecuadamente R+.
En el estudio que se presenta a continuación, llevado a cabo para verificar hasta qué punto la cadena más probable de la gramática (del lenguaje del autómata) está próxima a la cadena mediana, se tuvo que recurrir a un algoritmo en cierto modo similar al de Viterbi. La principal diferencia es que en este caso no se dispone de una cadena que determine qué transiciones escoger y cuándo terminar. No hay una etapa del trellis por cada símbolo de una cadena a reconocer, sino que se genera una nueva etapa cada vez que los caminos a través del autómata progresan de una transición a la siguiente. Se mantiene una lista de estados activos en la etapa anterior (un estado se puede activar más de una vez, a medida que van llegando a él caminos de distintas longitudes y total acumulado mayor al actual del estado). En cada iteración se escoge como camino máximo para un estado el que provenga de un estado activo y tenga el mayor total acumulado, si éste es mayor que el actual del estado. Se termina cuando el único estado activo sea el final. El máximo número de iteraciones viene dado por la longitud del camino más largo del grafo.
Como alternativa a este proceso, relativamente costoso (aunque menos que el propuesto por kohonen), se han estudiado dos definiciones: la cadena más frecuente y la cadena localmente más frecuente, que permiten obtener aproximaciones a la cadena más probable de una gramática, pero utilizando algoritmos de coste (en el segundo caso muy) inferior y proporcionando, en ocasiones, mejores resultados.
La secuencia de transiciones más frecuente es aquel camino en el autómata (cadena del lenguaje) que maximiza la suma de las frecuencias de utilización por R+ de las transiciones (reglas) que utiliza.
Sean fc(ri)=i=1..k, las frecuencias de las k transiciones (reglas) que utiliza el camino C[propersubset]C(p,f), donde C(p,f) son todos los caminos que van de p (el axioma) a f (el estado final del autómata[1]). La secuencia de transiciones más frecuente viene dada por:
La cadena localmente más frecuente es en realidad un procedimiento extremadamente subóptimo para obtener la cadena más frecuente: se empieza desde el estado inicial (o final si el autómata está representado de atrás hacia delante), y se escoge como estado siguiente aquel al que lleva la transición (regla) con más frecuencia en R+ (mayor f(r)); se repite esto mismo hasta llegar al estado final. Este procedimiento no implica ninguna optimización global y es por lo tanto extremadamente rápido y sencillo de implementar, habiendo proporcionado resultados extremadamente buenos (véase apartado siguiente).
Se llevaron a cabo una serie de experimentos para estudiar el buen comportamiento de las definiciones anteriores. En todos los casos se partió de grafos (autómatas) generados por ECGI a partir de muestras sintéticas. Estas cadenas sintéticas (palabras escritas con letras mayúsculas) se generaron produciendo errores aleatorios sobre una cadena dada (50% de distorsión: tantos errores como la mitad del número de caracteres de la cadena). Los errores eran los clásicos de borrado, inserción y substitución. El conjunto de símbolos insertables o que sustituían a otro estaba formado por las 26 letras mayúsculas inglesas (ni CH,Ñ,LL,RR ni acentos). El procedimiento de distorsión era sencillo: dado el porcentaje de distorsión se obtiene el número de errores a provocar; se escoge entonces al azar la posición y el tipo de error para cada uno de ellos.
Se hizo en todos los casos la suposición de que la cadena media del conjunto de muestras era la cadena original. Esta suposición es bastante plausible, dado el método de generación de las cadenas, sobre todo cuando el número de muestras es grande. Las palabras alteradas se escogieron arbitrariamente, en principio con el único criterio de que fueran de longitud diferente entre sí (aunque tres de ellas son las mismas que utiliza [Kohonen,85]). Fueron, en orden creciente de longitud: "IAPR", "HECTOR", "HELSINKI" y "RECOGNITION". Se generaron 4 autómatas para cada palabra, a partir de conjuntos formados por respectivamente 10, 20, 50 y 100 muestras alteradas; esto permitió comprobar si las definiciones eran válidas independientemente del tamaño de los autómatas y si su comportamiento mejoraba al aumentar la cantidad de información frecuencial disponible. En la figura 11.3 se muestran los conjuntos de 10 cadenas utilizados para generar los 4 primeros autómatas.
CIANR HETCR CHEINNI RGFKFGNITION
IAP HEPTOR HLELSIKI RECOXSNIIMOI
IAPI HECTOR HESENKC RIECOXGNIFON
LAPR HEVOR VELSKKI JEOGNITIGQN
ILP HETUOR CEELTSINKMI RESONIGIOR
RIAPR HSCOR ELNSGXNKI REOINITIGGN
IALR HTUCTOR GBHEKLSINK RCIORGNITVIHN
IAR FJHECTO HTOSINI RECOGNIN
IAPD GETOQR HXLSIKY ECOTNRITIIN
IUAR HETOFR HEKLUSNKK GRECPOGINITKO
Los resultados obtenidos en los experimentos son extremadamente esperanzadores. La cadena más probable proporciona la cadena original en el 56% de los casos estudiados (9 de 16), la cadena más frecuente la proporciona en el 62% de los casos examinados (10 de 16), siendo notablemente la mejor definición la versión subóptima de esta última, la cadena más frecuente por transiciones, la que proporciona la cadena original en 87% de los casos (14 de 16). Con las tres definiciciones (y sobre todo con la última) los resultados mejoran al aumentar el número de muestras (y por lo tanto la información contenida en el autómata), proporcionando las tres la cadena original cuando se aprende el autómata con 100 muestras. Como referencia, en la tabla 11.2 se muestran todos los resultados correspondientes a la palabra "HELSINKI". En la tabla 11.3 se muestran las cadenas localmente más frecuente obtenidas en los experimentos. Obsérvese que sólo en dos casos se ha producido un error con respecto a las cadenas originales.
Cadena más frecuente localmente: HELSINKI
Cadena más frecuente: HELSINKI
Cadena más probable: HEINNI
HELSINKI (20 cadenas ruidosas)
Cadena más frecuente localmente: HELSINKI
Cadena más frecuente: HEBELSINNKLMI
Cadena más probable: HELJNK
HELSINKI (50 cadenas ruidosas)
Cadena más frecuente localmente: HELSINKI
Cadena más frecuente: HELSSINKI
Cadena más probable: HELSINKI
HELSINKI (100 cadenas ruidosas)
Cadena más frecuente localmente: HELSINKI
Cadena más frecuente: HELSINKI
Cadena más probable: HELSINKI
Palabra NºMuestras CLMF
HELSINKI 10 HELSINKI
HELSINKI 20 HELSINKI
HELSINKI 50 HELSINKI
HELSINKI 100 HELSINKI
IAPR 10 IAR
IAPR 20 IAPR
IAPR 50 IAPR
IAPR 100 IAPR
RECOGNITION 10 RECOGNITION
RECOGNITION 20 RECOGNITION
RECOGNITION 50 RECOGNITITION
RECOGNITION 100 RECOGNITION
HECTOR 10 HECTOR
HECTOR 20 HECTOR
HECTOR 50 HECTOR
HECTOR 1000 HECTOR
En conclusión, la cadena localmente más frecuente, obtenida de manera simple, proporciona un procedimiento muy directo y de muy baja complejidad para obtener una buena aproximación a la cadena más probable (y por lo tanto, en muchos casos, a la mediana), no sólo del lenguaje de un autómata inferido por ECGI, sino también del conjunto de muestras R+, utilizadas para su construcción. Nótese sin embargo que un estudio más completo (utilizando mucho mayor número de palabras, de muestras y variando la distorsión) sería conveniente para centrar mejor los márgenes de funcionamiento del método.
La proximidad de la cadena más probable a la cadena mediana en la gran mayoría de los casos estudiados, proporciona además una demostración empírica de que el ECGI generaliza de manera progresiva y homogénea alrededor del conjunto de muestras, manteniendo el "centro de gravedad" del lenguaje (según Levenshtein y las probabilidades) próximo al centro del conjunto de muestras.
Como muestra práctica de ello, se adjuntan (figuras 11.4 y 11.5) la representación gráfica de las cadenas localmente más frecuentes de los lenguajes de algunos (uno por clase) de los autómatas inferidos durante los experimentos con dígitos manuscritos e impresos (rejilla 6).
Figura 11.5 Cadenas localmente más frecuentes de los lenguajes de 10 autómatas (uno por clase) inferidos por ECGI a partir de imágenes de dígitos impresos (rejilla 6)
[1] Recuérdese que los autómatas generados por ECGI sólo tienen un estado final. La definición es inmediatamente generalizable a un caso en el que existieran múltiples estados finales.