En los capítulos anteriores se ha comprobado que la complejidad espacial de los modelos que infiere ECGI, sin ser excesiva, es suficientemente grande para que en algunos casos represente una penalización. En este capítulo se presenta una metodología de simplificación de autómatas, que autoriza reducir la complejidad espacial (y por lo tanto la complejidad temporal en reconocimiento) de los modelos inferidos en más de un 40%, sin merma apreciable en la eficacia del reconocimiento efectuado con dichos modelos.
El método de simplificación se basa tanto en la información estadística aportada por la extensión estocástica de ECGI, como en ciertas propiedades estructurales de los autómatas (gramáticas) inferidos: el tráfico por estado y/o el tráfico por transición. La definición de estos tráficos se basa directamente en en el concepto de caminos en un grafo sin circuitos, al cual se dedican los primeros apartados de ese capítulo.
En los siguientes apartados se presentan una serie de algoritmos que permiten un análisis de las propiedades estructurales de un grafo dirigido y sin circuitos (DAG: "directed acyclic graph" [Aho,73]), concentrándose principalmente de aquellas relacionadas con los caminos que van de un vértice a otro a través de dicho grafo. En todo lo que sigue se tratará con un grafo dirigido G=(V,A); A={(u,v): u[propersubset]V, v[propersubset]V}[subset]V2.
Se define el número de caminos en G, que van desde el vértice p (principio del camino) a un vértice u; p,u[propersubset]V como:
El número de caminos inversos en G, que llegan a p desde u (que van de u a p), se obtiene simplemente invirtiendo el sentido de las aristas y efectuando el cálculo al revés:
El Tráfico entre p y f (final del camino) que pasa u; p,f,u[propersubset]V, es decir, el número de caminos en G que, yendo de p a f, pasan por u, se define simplemente como (figura 10.1):
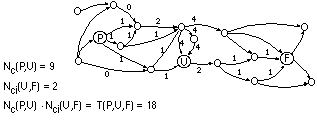
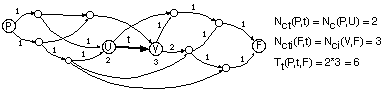
A partir de la definición del número de caminos que llegan a un vértice u de G provenientes de otro p, Nc(p,u), se obtiene inmediatamente el número de caminos que pasan por la arista t=(u,x)[propersubset]A, viniendo del vértice p[propersubset]V:
Similarmente, el número de caminos inversos que pasan por la arista t=(u,v), viniendo del vértice p será:
Para obtener el camino más largo en G que va de p a f, es decir, el que tiene el mayor número de vértices, se puede utilizar la recurrencia:
El camino en G, que va de p a f y que tiene el mayor número de transiciones es el mismo que Cl(p,f), ya que el número de transiciones de un camino siempre es uno menos que el de vértices.
El camino más corto en G que va de p a f, es decir, el que tiene menor número de vértices, se obtiene con la misma recurrencia, sólo que minimizando en vez de maximizar. Escribiremos Cc la longitud del camino más corto.
Aplicando una típica transformación recursivo-iterativa es posible calcular eficientemente las cantidades definidas en los apartados anteriores, evitando recalcular cantidades ya obtenidas:
Algoritmo Caminos
Datos G=(V,A) /* Grafo */
p,f[propersubset]V /* vértices inicial y final */
Resultado Total:R
Auxiliar sig:V->V /* orden en V */
Variables
x,u[propersubset]V
Acum:CVxR /* vector indexado por V */
Inicialización
u:=p; Acum[p]:=1
Método
mientras u!=f hacer
u:=sig(u); Acum[u]:=0
A x:(x,u)[propersubset]A hacer /* predecesores de u */
Acum[u]:= Acum[u] + Acum[x]
fin A
fin mientras
Total:=Acum[f]
fin Caminos
Este algoritmo proporciona el número de caminos que llegan desde p a todos los vértices a los que llega un camino desde p.
Obsérvese que se ha utilizado el orden topológico del conjunto de vértices, que asegura que todos los predecesores de un estado son anteriores a él, lo cual siempre es posible si el grafo no tiene circuitos (ver capítulo 5: corrección de errores). Gracias a este orden se ha podido obtener el resultado con un único recorrido de los vértices.
El algoritmo presentado obtiene el número de caminos Nc(p,f). El número de caminos inversos Nci(f,p) se calcula con el mismo algoritmo, pero sumando sobre los sucesores y empezando por f. Esto obligará en general a invertir la representación del grafo, puesto que usualmente se representan las aristas como una lista de predecesores (sucesores).
La obtención de Cl y Cc recurre al mismo algoritmo, solo que maximizando o minimizando en vez de sumar.
Obsérvese que el método utilizado para calcular el tráfico, que requiere un barrido de programación dinámica hacia delante (Nc(p,u)) y otro hacia detrás (Nci(u,f)) de un grafo dirigido sin circuitos, está basado en la misma idea que el algoritmo Forward-Backward utilizado habitualmente para la estimación de probabilidades en modelos de Markov.
A partir del tráfico por vértice (arista), asumiendo la existencia en el grafo G de dos vértices privilegiados[1] p,f[propersubset]V y siendo ti=(u,xi)[propersubset]A, i=1..m las aristas que tienen por origen el vértice u, es posible definir la probabilidad estructural de una arista ti:
Proposición: Si cpf es el conjunto de caminos de p a f en G, definimos la probabilidad estructural de un camino C[propersubset]cpf, formado por la secuencia de k aristas t1,t2..tk; como:
PE(C)= . ..... =
. ..... =
= c.q.d.
Es decir, la probabilidad estructural de cualquier camino de p a f es:
De la anterior proposición también es posible deducir que si, en un autómata estocástico sin circuitos, todas las probabilidades de las transiciones son iguales a las probabilidades estructurales de las aristas del grafo que representa el autómata, entonces todas las cadenas del lenguaje del autómata tienen la misma probabilidad. Eso sí, si el autómata es ambiguo una cadena podrá ser tanto más probable cuanto más caminos en el autómata -en su grafo- reconozcan dicha cadena.
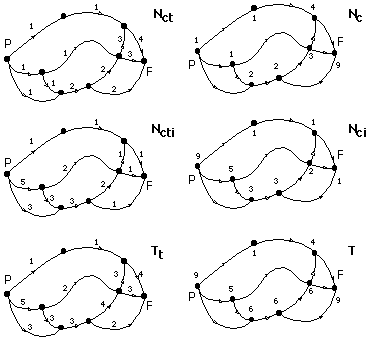
Una medida de la importancia de una arista t y de un vértice u, relativa al número de caminos puede definirse de la forma:
Tal como se expuso, en el apartado dedicado a su convergencia, el método ECGI infiere en general autómatas muy compactos (un orden de magnitud más reducidos que el autómata canónico). Sin embargo, ello sigue implicando una gran cantidad de información (a veces hasta 300 estados por autómata), costosa de utilizar en los análisis sintácticos requeridos en la fase de reconocimiento.
Por otra parte, durante el reconocimiento, ECGI nuevamente superpone a la gramática inferida un modelo de error, siendo más que probable que parte de éste duplique parte del que se ha incluído durante la inferencia de la misma estructura. Además, como se ha comprobado durante la exposición de los heurísticos en los que se fundamenta ECGI, ocurre a veces que se incluyan en la estructura estados y transiciones redundantes.
Todo ello induce a pensar que es posible suprimir cierta parte de los estados y transiciones del modelo inferido, sin por ello mermar su poder de reconocimiento. En esta línea, exponemos a continuación una serie de técnicas que se pueden utilizar para este fin y mostraremos cómo con ellas se ha conseguido reducir los autómatas hasta un 30%.
El algoritmo utilizado para la simplificación de los autómatas generados por ECGI puede resumirse en una frase: "quitar cada vez el estado menos significativo y repetirlo hasta que se haya conseguido la simplificación requerida".
Evidentemente, ello no es tan simple como parece:
* Hay que definir lo que se entiende por "estado menos significativo"
* Existen varios criterios posibles para decidir cuando la
simplificación es suficiente.
* Al suprimir un estado es necesario asegurarse de que no se modifica la
calidad de "estado menos significativo" o reestimarla. Asimismo hay que
realizar la supresión en cadena de aquellos estados que han quedado
desconectados (sin predecesores y/o sucesores) al quitar otro.
Una herramienta decisiva para todo ello es el tráfico por nodo, definido anteriormente.
Para defnir "el estado menos significativo" qx se han probado tres posibilidades (qp y qf son el estado final e inicial respectivamente):
* El estado de menos tráfico
T(qp,qx,qf).
* El estado menos probable, es decir, el menos frecuentemente utilizado por
R+ (menor f(qx)).
* La combinación de ambos criterios anteriores: el estado con menor
producto T(qp,qx,qf).f(qx).
Como se ha mostrado anteriormente, T(qp,qx,qf) está relacionado con la importacia estructural de qx, es decir, la importancia de qx para la variedad y tamaño del lenguaje inferido. Por su parte, f(qx) está directamente relacionado con la importancia de qx para R+, y por lo tanto para las cadenas de lenguaje real. Ambos criterios son complementarios y es difícil que se pueda decidir cuál es el mejor, lo que justifica la tercera definición.
Para detener la simplificación se han adoptado dos puntos de vista distintos, el algoritmo se detendrá cuando:
* Se haya suprimido un determinado porcentaje (de cadenas distintas) del
lenguaje original.
* Se hayan borrado un determinado porcentaje de los estados del
autómata original.
El primer punto es un límite abstracto, directamente relacionado con la generalización que se le permite al modelo. El segundo es un límite concreto, que limita la complejidad espacial (temporal) de la representación. Ambos están muy relacionados, aunque la simplificación por estados es más fácil de controlar (téngase en cuenta que suprimir el 99% del lenguaje aún nos deja con aproximaamente el 50% de los estados, dada la relación exponencial entre tamaño de lenguaje y número de estados).
En la práctica, los porcentajes de estados o cadenas del lenguaje a mantener se deberán estimar empíricamente y dependerán muy fuertemente de la tarea concreta de reconocimiento a la que estén abocados los modelos finales.
El algoritmo concreto de simplificación es el siguiente (transcripción directa del implementado):
Algoritmo Simplifica
Datos A=(V,Q,d,qp,qf) /* Autómata a simplificar */
umbral:Z
Resultado As=(V,Qs,ds,qp,qf) /* el mismo, simplificado */
Auxiliar /* [tau] es el tipo "estado" */
criterio:[tau]->R /* según simplificación */
Variables qx : [tau]
Método
/* borrado de estados sobrantes */
repetir
ObtenerTráfico(A); Nc(qp,qf):=T(qp)
si Nc(qp,qf) > umbral entonces
qx :=
borrar(qx)
hasta Nc(qp,qf)<=umbral;
/* borrado de desconectados */
ObtenerTráfico(A)
A q[propersubset]Q si T(q)=0 entonces borrar(q)
fin simplifica
El algoritmo mostrado utiliza como criterio de detención el tamaño del lenguaje. Es obvia la modificación que sería necesaria para detenerlo por número de estados. En cada caso habrá que calcular el umbral correspondiente a partir de |Q| o Nc(qp,qf) iniciales.
Se ha utilizado la particularidad evidente de que todos los caminos que van de qp a qf pasan por qp, es decir, se ha obtenido Nc(qp,qf) como T(qp). La reobtención del tráfico a cada iteración es imprescindible, incluso aunque no se le utilize en ningún criterio, para poder asegurarse de no borrar un estado por el que pasan todos los caminos (lo que puede ocurrir si se lleva la simplificación demasiado lejos). Ello se comprueba en la búsqueda del estado que cumple el criterio de simplificación, asegurándose de no escoger un estado que no se puede borrar.
Nótese que la segunda etapa del algoritmo es la que borra todos los estados que han quedado desconectados, es decir cuyo tráfico es nulo.
Obviamente, borrar(q) también borra las transiciones que llegan (van) a q. Ello altera la cuenta de los caminos que salen de q, por lo que la normalización efectuada en la extensión estocástica deja de ser consistente. Para recuperar la consistencia sería necesario un barrido del autómata final, en el que se igualan de nuevo las frecuencias de los nodos a la suma de las transiciones que les llegan y se vuelve a normalizar.
El algoritmo recurre repetidamente a la evaluación del tráfico. Es por lo tanto imprescindible disponer en todo momento del autómata y de su inverso (con las transiciones invertidas) con el fin de poder efectuar los barridos hacia delante y hacia detrás.
Aunque se ha implementado ambas técnicas de detener la simplificación, todos los experimentos se han llevado a cabo únicamente simplificando por tamaño de lenguaje, ya que esta es una medida más relacionada con la semántica del modelo a simplificar. En todos los casos, las tasas de reducción por estados que se proporcionan se han medido a posteriori.
En 3 de los experimentos realizados con los dígitos hablados H1, H5 y H6 (ver detalles en capítulo 8) se han simplificado los 10 autómatas representativos de cada dígito y se ha repetido el reconocimiento. Recuérdese que todos los experimentos son multilocutor y la única diferencia entre H5 y H6 es un locutor en aprendizaje, notablemente diferente a los demás, en H5. H1 utiliza 5 locutores (10 muestras de cada locutor por dígito) en aprendizaje y 5 en reconocimiento. H5 y H6 utilizan 6 y 4 respectivamente. Para H6 son 6 locutores. En todos los casos se utilizó el modelo de error completo en reconocimiento. Como criterio de estado menos significavo se ha utilizado la combinación T(qp,qx,qf).f(qx).
La simplificación se ha efectuado en tres etapas, cada una de las cuales significaba cada vez reducir de un 99% el lenguaje del autómata de la anterior.
H1 1533 99,2 98 96 94,4
H5 1712 100 99,75 99,75 94,5
H6 1587 100 100,0 99,3 97,5
En la tabla es posible comprobar cómo en la mayoría de los casos los resultados empeoran sólo ligeramente o nada en absoluto cuando se suprime el 99% del lenguaje (el autómata queda con un 40% de estados), lo cual implica que realmente existe mucha información redundante en los autómatas, sobre todo cuando el aprendizaje ha sido suficiente como en el caso de H6.
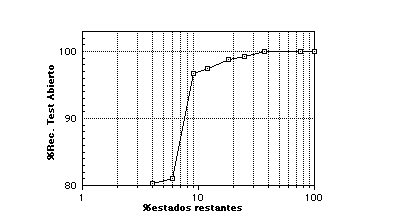
Para poder estimar cómo empeora la tasa de reconocimiento en función de la simplificación aplicada, se completó el experimento H6 reduciendo progresivamente el tamaño del lenguaje, midiendo cada vez la tasa de reconocimiento y el porcentaje de estados restantes respecto al autómata original. Representando los valores obtenidos se consiguió la curva de la figura 10.4.

Los errores en este caso empiezan entre un 37% y 25% de estados restantes (67 a 49 estados de media), y la tasa de reconocimiento nunca desciende por debajo del 80%, incluso cuando sólo quedan un 15% de los estados de los autómatas (24 estados de media). El emporamiento de la tasa de reconocimiento es muy lento, hasta un cierto punto (alrededor de un 20% de estados) en el cae bruscamente, probablemente debido a que en ese punto se suprimen partes de los lenguajes que diferencian las clases, y no sólo pequeñas variaciones de las que puede dar cuenta el modelo de error empleado en reconocimiento.
T(q) 97,5 97 93,75
f(q) 99,5 99,5 94,25
T(q).f(q) 100,0 99,3 97,5
Los resultados presentados demuestran que es muy factible simplificar los autómatas inferidos por ECGI sin afectar significativamente la tasa de reconocimiento. El porcentaje de simplificación admisible depende en gran manera de la tarea concreta a la que se aplicarán los autómatas resultantes, pero se ha comprobado que si éstos están suficientemente bien aprendidos se puede llegar a suprimir más de un 50% de estados, pudiéndose incluso llegar a un 75%.
Nótese que una posible utilización, muy sugestiva, de la simplificación de autómatas, podría consistir en proporcionar la capacidad de "olvido" a un sistema que integrara la inferencia y reconocimiento: un aprendizaje indefinido lleva a la modelización de muchísimos errores por las mismas gramáticas, errores que se producen con muy poca frecuencia y que es superfluo tener "anotados". Una ligera simplificación, realizada cada cierto número de muestras durante el aprendizaje, permitiría suprimir de las gramáticas estos espúreos.
[1] Toda la discusión que sigue considera las propiedades del grafo únicamente en relación con los caminos que van de p a f.